Oberoende händelser

När du kastar en enkrona så är det #50 # % chans att få krona och #50 # % chans att få klave. Om du kastar myntet igen har chansen för krona eller klave inte ändrats. Detta kallas för en oberoende händelse.

Andra exempel på oberoende händelser är vid kast med tärning eller då man plockar en boll ur en burk, under förutsättning att det sker med återläggning.

Beroende händelser

Första gången vi drar en boll ur burken är #P({\text{blå}}) = \frac{3}{5}#. Om vi får en blå
boll, och inte lägger tillbaka den, och sen drar på nytt, är sannolikheten att vi får ytterligare en blå boll #P({\text{blå}}) = \frac{2}{4} = \frac{1}{2}#.

Resultatet blev ett annat, eftersom vårt föregående försök påverkade både de möjliga och de gynnsamma fallen. Vi säger att händelserna är beroende av varandra.

#\,#

#\,#

Utredning av händelser och träddiagram

Om vi kastar en enkrona två gånger så kan vi illustrera de olika utfallen med ett diagram.

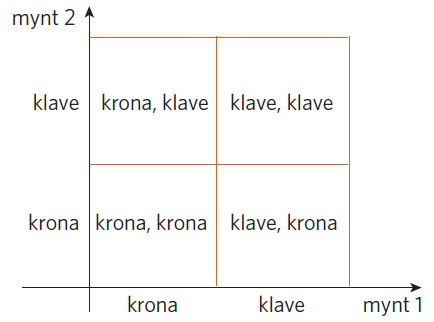
Händelsen att få krona båda gångerna har sannolikheten

#P({\text{krona}}{\text{,}}\,{\text{krona}}) = \frac{1}{4}#.

De fyra olika utfallen i utfallsrummet har tillsammans sannolikheten #1. # Den här metoden fungerar bra när två händelser kopplas ihop.

Vi kan även illustrera situationen med hjälp av ett träddiagram.

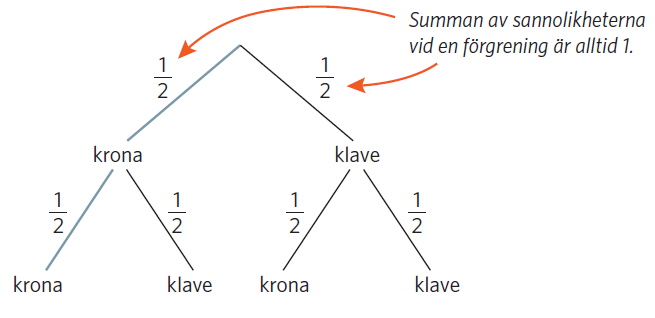
Om vi multiplicerar sannolikheterna för de två enskilda händelserna för krona får vi #P({\text{krona}}{\text{,}}\,{\text{krona}}) = \frac{1}{2} \cdot \frac{1}{2} = \frac{1}{4}#.

Vi multiplicerar alltså nedåt i en gren för att få sannolikheten för hela händelsen. Detta kallas ibland för "multiplikationsprincipen".

Principen kan användas oavsett hur många händelser som följer på varandra.

Om vi lägger ihop alla grenarna får vi

#P({\text{utfallsrummet}}) = \frac{1}{2} \cdot \frac{1}{2} + \frac{1}{2} \cdot \frac{1}{2} + \frac{1}{2} \cdot \frac{1}{2} + \frac{1}{2} \cdot \frac{1}{2} = 1#

Sannolikheterna för de olika grenarna adderas. Detta kallas för "additionsprincipen".

Ett träddiagram fungerar bra även med många händelser efter varandra.

#\,#

#\,#