1c 3. Förändringar och sannolikhet: 3.3 Sannolikhetslära
 Komplementhändelse
Komplementhändelse
Hur stor är sannolikheten att få minst en blå socka då man utan återläggning drar tre sockor ur högen?
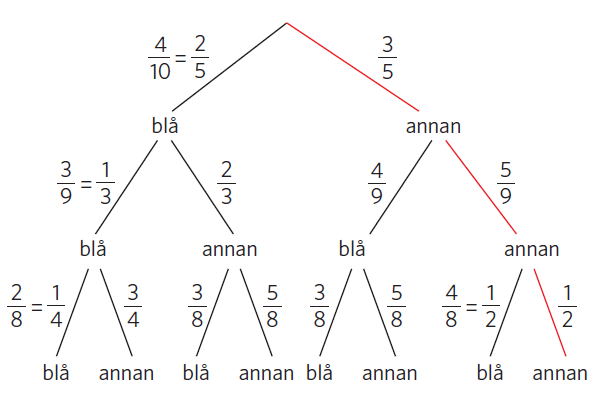
Vi ritar upp träddiagrammet.
Det finns #7 # gynnsamma utfall som innehåller minst en blå socka. Komplementhändelsen till detta är att inte få någon blå socka alls. Komplementhändelsen är färgmarkerad i träddiagrammet.
#P(\text{minst en blå socka}) + P(\textrm{ingen blå socka})= 1 #
eftersom dessa händelser tillsammans utgör hela utfallsrummet.
I stället för att räkna ut alla sju grenarna med blå socka räknar vi.
#P(\textrm{minst en blå socka}) = 1 - P (\text{ingen blå socka})#
#P({\text{minst en blå socka}}) = 1 - \frac{3}{5} \cdot \frac{5}{9} \cdot \frac{1}{2} = 1 - \frac{1}{6} = \frac{5}{6}#
Om händelserna A och B inte kan äga rum samtidigt och utgör hela utfallsrummet är B komplementhändelse till A och P #(# A) #+ # P #(# B) #= 1 #
|
Komplementhändelse Om händelser A och B inte kan äga rum samtidigt och utgör hela utfallsrummet gäller: Händelserna är varandras komplementhändelse #P(A) + P(B) =1# |
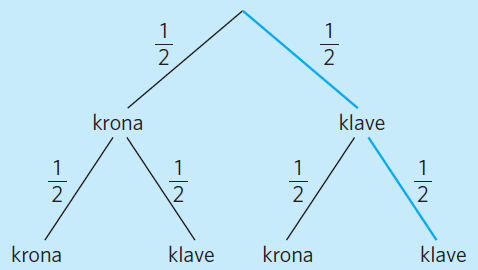
Vi använder den markerade komplementhändelsen "klave, klave":
#P{\rm{(klave}}{\rm{, klave)}} = \frac{1}{2} \cdot \frac{1}{2}#
#P{\rm{(minst en krona)}} = 1 - \frac{1}{2} \cdot \frac{1}{2} = \frac{3}{4}#
Komplementhändelsen är ingen vinst alls.
P #(# minst en vinst) #= 1 - 0,95^{20} ≈ 64,2 # %
Komplementet blir de två utfallen "att bara få lakritsbåtar" och "att bara få hallonbåtar". De två utfallen har samma sannolikhet eftersom det finns lika många av båda sorterna.
#P({\textrm{bara lakritsbåtar}}) = \frac{6}{{12}} \cdot \frac{5}{{11}} \cdot \frac{4}{{10}} \cdot \frac{3}{9} \cdot \frac{2}{8} \cdot \frac{1}{7} = \frac{1}{2} \cdot \frac{5}{{11}} \cdot \frac{2}{5} \cdot \frac{1}{3} \cdot \frac{1}{4} \cdot \frac{1}{7} = \frac{1}{{924}}#
#P({\textrm{minst}}\,{\textrm{en}}\,{\textrm{av}}\,{\textrm{varje}}\,{\textrm{smak}}) = 1 - 2 \cdot \frac{1}{{924}} \approx 99,8 \,\% #