|
Att köpa böcker hos "Bokgiganten" kostar #50 # kr per bok om du inte är medlem i deras bokklubb.
Kostnaden # y # för # x # böcker kan då skrivas:
#y=50x#

# y = 50 x # är en direkt proportionalitet. Oavsett hur många böcker du köper är genomsnittskostnaden #50 # kr.
En direkt proportionalitet uppfyller villkoret att grafen är en rät linje genom origo, det vill säga # y = 0 # då # x = 0. # Ett annat exempel på direkta proportionaliteter är kostnaden för lösgodis i affären, där priset är angivet per hekto. Om #1 # hg kostar #8 # kr betyder det att # x # hg kostar #8 x # kr.
Generellt skrivs direkta proportionaliteter #y= kx#. Proportionalitetskonstanten # k # är ett mått på linjens lutning i förhållande till # x #-axeln.
|
| #x# |
#y=50x# |
| #0# |
#0# |
| #1# |
#50# |
| #2# |
#100# |
#\qqquad#Grafen till #y=50x#

|
#\,#
|
a) Vilka av följande samband beskriver direkta proportionaliteter?
#y=3x#
#y=3x-2#
#y=-4x#
#y=-x+2#
|
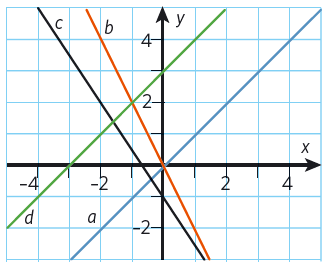
b) Vilka av graferna visar en direkt proportionalitet?
|
a) #y=3x# och #y=-4x#
b) #a# och #b#, de går genom origo.
#\,#
|
Proportionalitetskonstant
| Direkt proportionalitet: |
# \quad y = kx # |
| Proportionalitetskonstant: |
# \quad k = \frac{{y{\text{ - värdet}}}}{{x{\text{ - värdet}}}}# |
Proportionalitetskonstanten, "k-värdet", är ett mått på linjens lutning i förhållande till # x #-axeln. Grafen till en direkt proportionalitet är en rät linje som alltid går genom origo.
|
Bestäm sambandet mellan pris och vikt för bananer om #5 # kg bananer kostar #60 # kr.
#k = \frac{{60\,{\rm{kr}}}}{{5\,{\rm{kg}}}} = 12\,{\rm{kr/kg}}#
Svar: # y = 12 x , y # kr för # x # kg bananer.
En burk med #3 # kg inlagd gurka kostar #60 # kronor, medan en burk med #5 # kg kostar #75 # kronor. Är priset proportionellt mot antalet kg gurka?
#3#-kilosburk: #\frac{{60\,{\rm{kr}}}}{{3\,{\rm{kg}}}} = 20\,{\rm{kr/kg}}#
#5#-kilosburk: #\frac{{75\,{\rm{kr}}}}{{5\,{\rm{kg}}}} = 15\,{\rm{kr/kg}}#
Svar: Nej, priset är inte proportionellt mot antalet kg gurka eftersom kilopriset ändras.
 Direkt proportionalitet
Direkt proportionalitet



