1c 4. Funktioner: 4.3 Linjära samband
 Linjära samband och räta linjens ekvation
Linjära samband och räta linjens ekvation
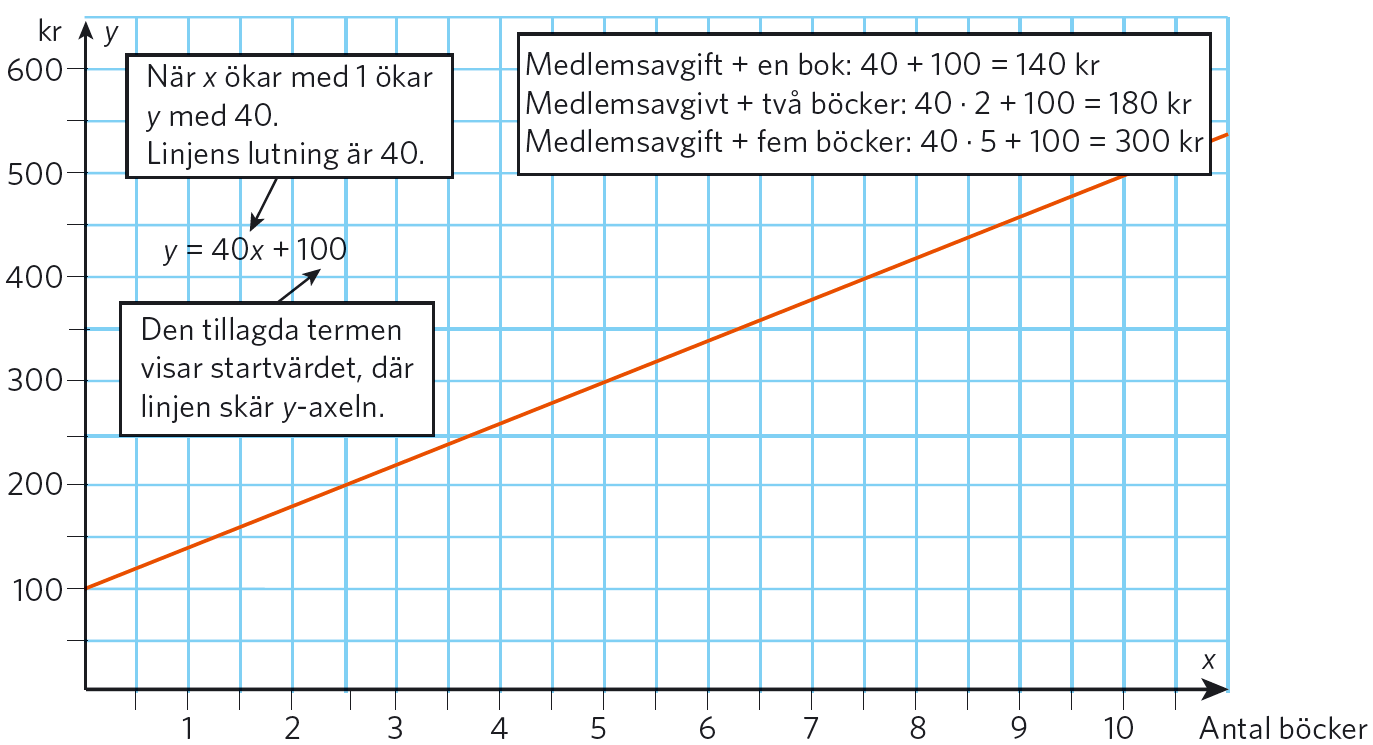
En bokklubb har en medlemsavgift på #100 # kronor per år. Som medlem får man köpa böcker för #40 # kronor styck. Om man köper # x # böcker på ett år blir kostnaden
#\quad y = 40 x + 100 #
Vi gör en värdetabell och ritar grafen.
| #x# | #y=40x+100# |
| #0# | #100# |
| #5# | #300# |
| #10# | #500# |
Av figuren framgår att grafen till funktionen # y = 40 x + 100 # är en rät linje. Koefficienten framför # x , # det vill säga #40, # är linjens lutning eller riktningskoefficient. För varje bok vi köper ökar kostnaden med #40 # kr. Riktningskoefficienten brukar betecknas # k . #
Vi ser också att när # x = 0 # är # y = 100. # Om vi sätter in # x = 0 # i funktionsuttrycket försvinner den första termen och endast konstanttermen, #100, # blir kvar. Linjens skärningspunkt med # y #-axeln brukar betecknas # m . #
Alla samband på formen # y = kx + m # har grafer som är räta linjer. De kallas därför linjära samband. # k # är linjens riktningskoefficient. # m # är # y #-koordinaten för linjens skärningspunkt med # y #-axeln. Om # m = 0 # är # y # direkt proportionell mot # x . #
Sambandet # y = kx + m # kallas också för räta linjens ekvation.
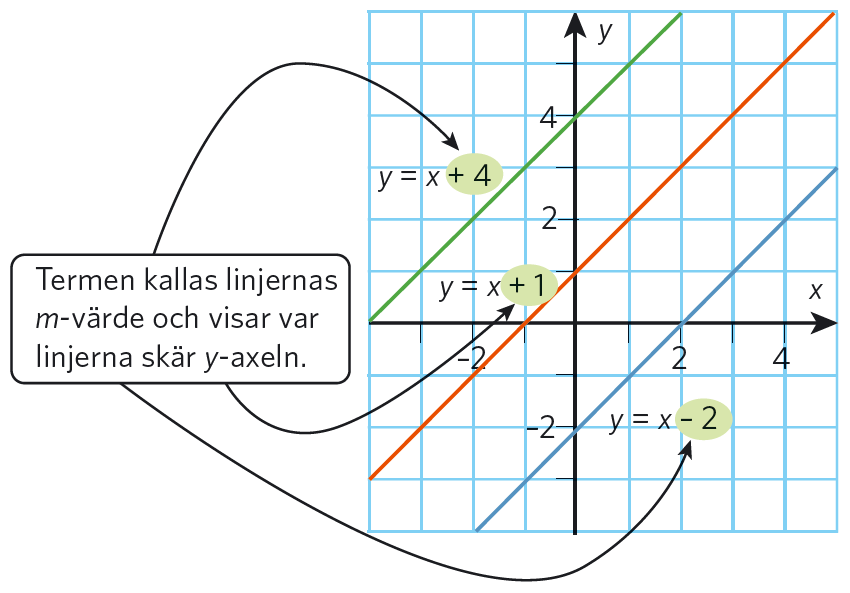
# m #-värdet
Vi ritar tre parallella linjer med hjälp av värdetabeller
I den punkt där linjen skär # y #-axeln är # x = 0#, det vill säga # y = k \cdot 0+m = m #.
#\,#
Kontroll
#\,#
#\,#
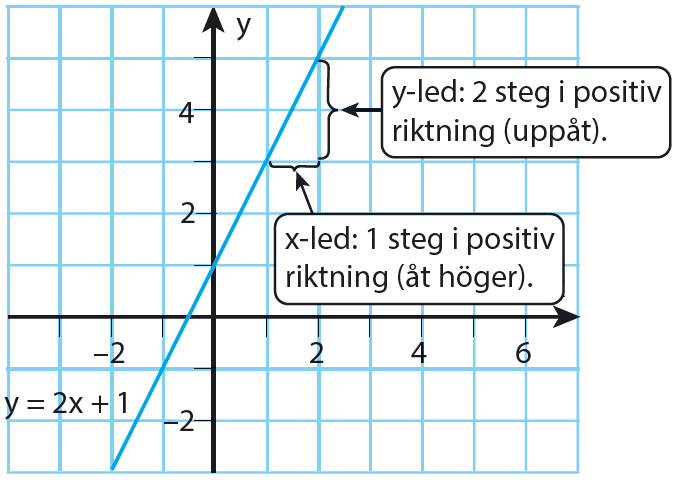
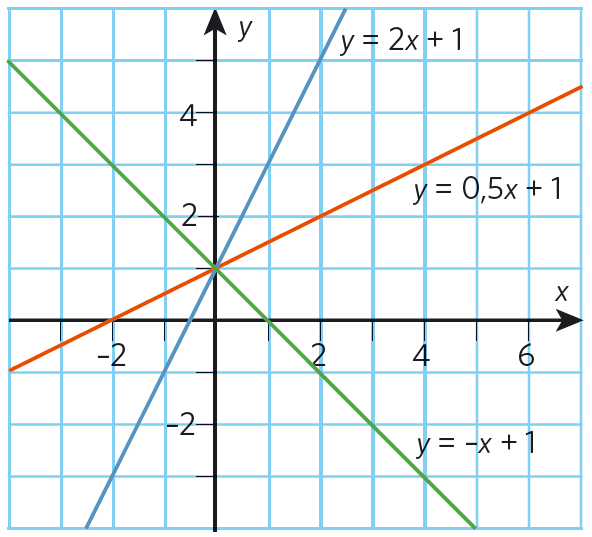
Vi utgår från punkterna @(1, 3)@ och @(2, 5)@ som båda ligger på linjen. Om vi har koordinaterna för två punkter på en linje kan vi använda dessa för att bestämma linjens lutning:
Ändringen i #y#-led är #5-3=2#, så #\Delta y = 2#.
Ändringen i #x#-led är #2-1=1#, så #\Delta x = 1#.
Här gäller @k = (\Delta y)/(\Delta x) = 2/1 = 2@. Ett positivt #k#-värde innebär att #y#-värdet ökar då #x# ökar. Man säger att "linjen har positiv lutning" om @k > 0@.
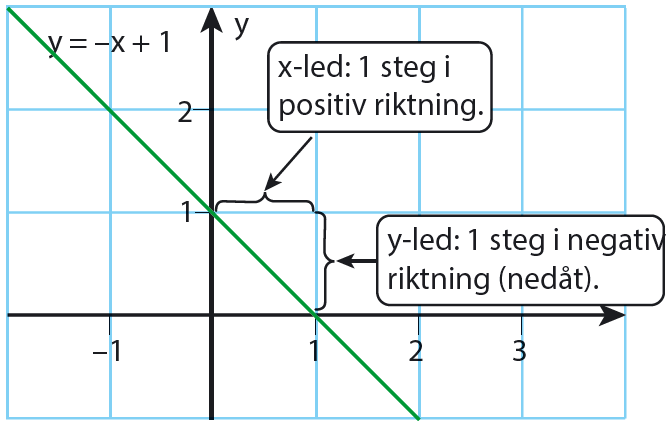
Nedan har vi linjen @y = -x + 1@
Här utgår vi från punkterna @(0, 1)@ och @(1, 0)@.
Ändringen i #y#-led är @Δy = 0 – 1 = –1@.
Ändringen i #x#-led är @Δx = 1 – 0 = 1@.
@k = (\Delta y)/(\Delta x) = -1/1 = -1@. Ett negativt #k#-värde innebär att #y#-värdet minskar då #x# ökar. Man säger att "linjen har negativ lutning" om @k < 0@.
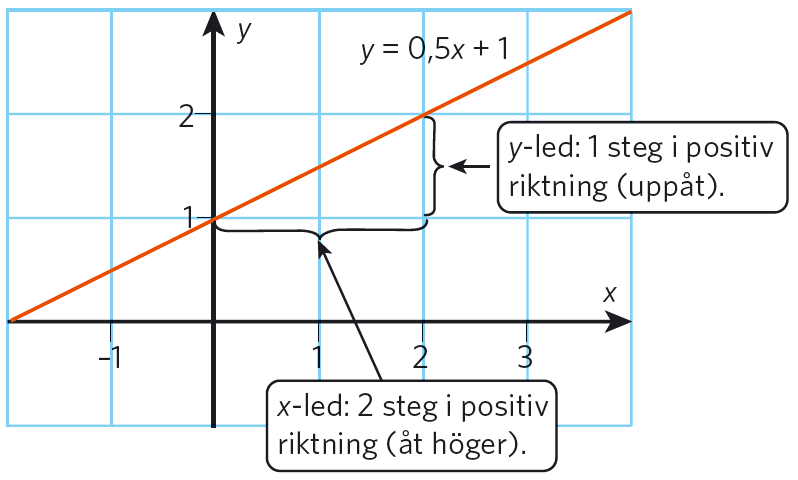
I nästa koordinatsystem visas linjen @y = 0,5x + 1@.
Vi utgår från punkterna @(0, 1)@ och @(2, 2)@.
@k = (\Delta y)/(\Delta x) = (2-1)/(2-0) = 1/2 = 0,5@
Även denna linje har positiv lutning.
#\,#
Kontroll
#\,#
Två viktiga linjer
För att kunna beskriva alla räta linjer som kan dras i ett koordinatsystem behöver vi också kunna beskriva linjer som är parallella med koordinataxlarna.
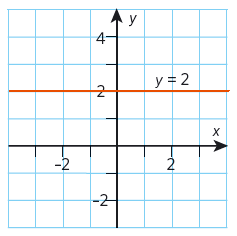
Linjen # y = m#, där # m # är konstant, är parallell med # x #-axeln.
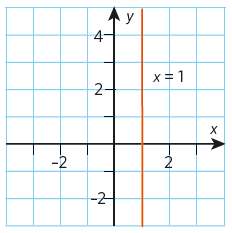
Linjen # x = a#, där # a # är konstant, är parallell med # y #-axeln.
|
Räta linjer Räta linjens ekvation på #k#-form: # y = kx + m # # m # anger var grafen skär # y #-axeln. # k # är riktningskoefficienten som anger linjens lutning: #k = \frac{{{\text{ändring i }}y{\text{ - led}}}}{{{\text{ändring i }}x{\text{ - led}}}} = \frac{{\Delta y}}{{\Delta x}}# Ett positivt # k #-värde innebär att # y #-värdet ökar då # x # ökar. Ett negativt # k #-värde innebär att # y #-värdet minskar då # x # ökar.
|
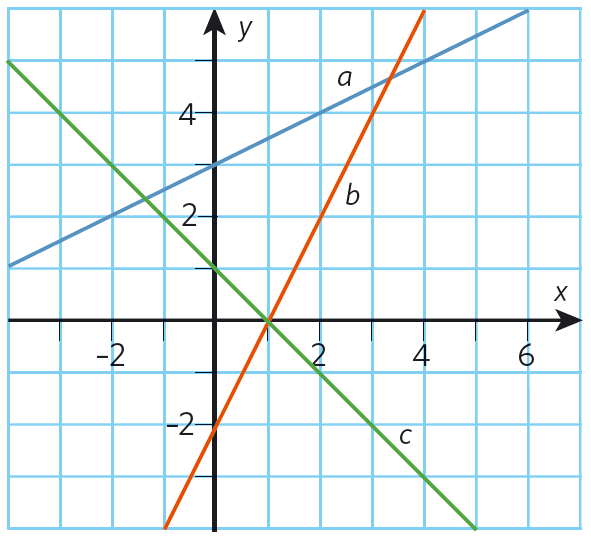
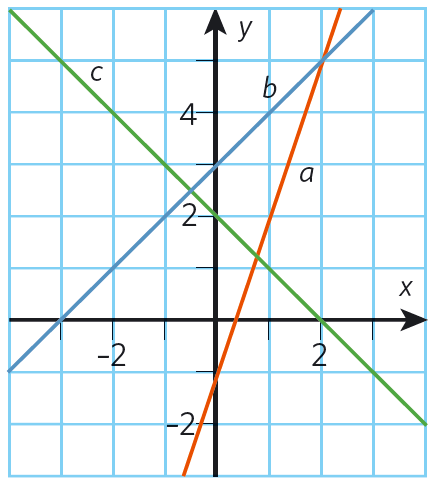
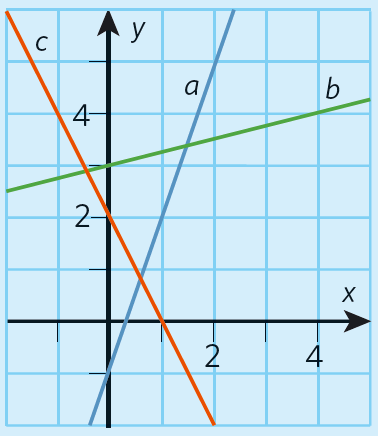
Linje # a #
Linjen skär # y #-axeln i punkten #(0, -1), # det vill säga # m = -1. #
Placerar vi pennan i punkten #(0, -1) # och går ett steg åt höger i # x #-riktningen måste vi gå #3 # steg uppåt i # y #-riktningen för att komma tillbaka till linjen, det vill säga Δ # x = 1 # och Δ # y = 3#.
#k = \frac{{\Delta y}}{{\Delta x}} = \frac{3}{1} = 3#
Svar: # y = 3 x - 1 #
Linje # b #
Placerar vi pennan i #(0, 3) # ser vi att vi måste gå #4 # steg åt höger i # x #-riktningen för att kunna ta #1 # steg i # y #-riktningen så att vi är tillbaka på linjen.
#\Delta x = 4 # och # \Delta y = 1 #
#k = \frac{{\Delta y}}{{\Delta x}} = \frac{1}{4}#
Svar: #y = \frac{1}{4}x + 3 = 0,25x + 3#
(Man får oftast välja vilket av svarsalternativen man vill)
Linje # c #
För varje positivt steg i # x #-riktningen går vi #2 # steg i negativ # y #-riktning.
#k = \frac{{\Delta y}}{{\Delta x}} = \frac{{ - 2}}{1} = - 2#
Svar: # y = -2 x + 2 #
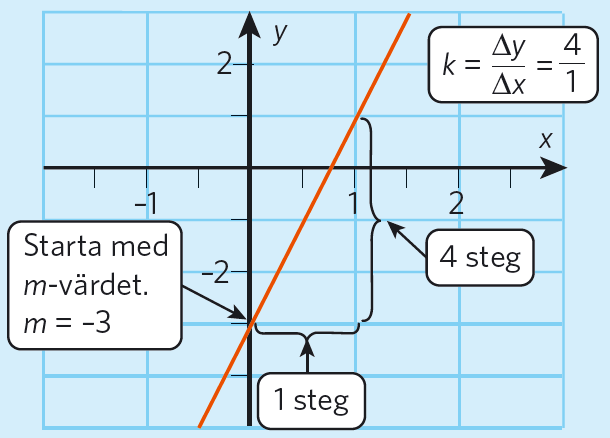
Sätt ut skärningspunkten med # y #-axeln. # y = -3#, eftersom # m = -3#.
Använd riktningskoefficienten, # k #-värdet, för att hitta en punkt till.
Dra linjen genom de två punkterna.