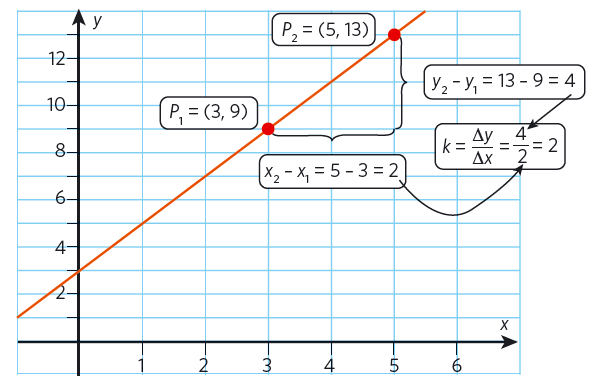
Om två punkter på en linje är kända går det att algebraiskt bestämma en linjes ekvation. Linjen i figuren går igenom punkterna @(3, 9)@ och @(5, 13)@.

Vi kan beräkna # k #-värdet utan att rita:

#k = \frac{{\Delta y}}{{\Delta x}} = \frac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}} = \frac{4}{2} = 2#

Vi beräknar # m #-värdet genom att sätta in # k #-värdet och valfri punkt i räta linjens ekvation:

# y = kx + m = 2 # och punkten @(3, 9)@ sätts in.

#9 = 2 \cdot 3 + m #

# m = 9 - 6 #

# m = 3 #

Linjens ekvation är # y = 2 x + 3#.

På motsvarande sätt bestämmer vi ekvationen för den räta linje som går genom punkterna #(-1, \,5) # och #(3, \,17)#.

Först bestämmer vi # k #-värdet:

#k = \frac{{\Delta y}}{{\Delta x}} = \frac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}} = \frac{{17 - 5}}{{3 - ( - 1)}} = \frac{{12}}{4} = 3#

Sedan sätter vi in # k #-värdet och en punkt i räta linjens ekvation:

# y = kx + # m #= 3 # och punkten #(-1, \,5) # sätts in.

#5 = 3 \cdot (-1) + m #

#5 = -3 + m #

# m = 8 #

Linjens ekvation är # y = 3 x + 8#.

#\,#

#\,#

#\,#