1c 4. Funktioner: 4.4 Funktioner av olika slag
 Exponentialfunktioner
Exponentialfunktioner
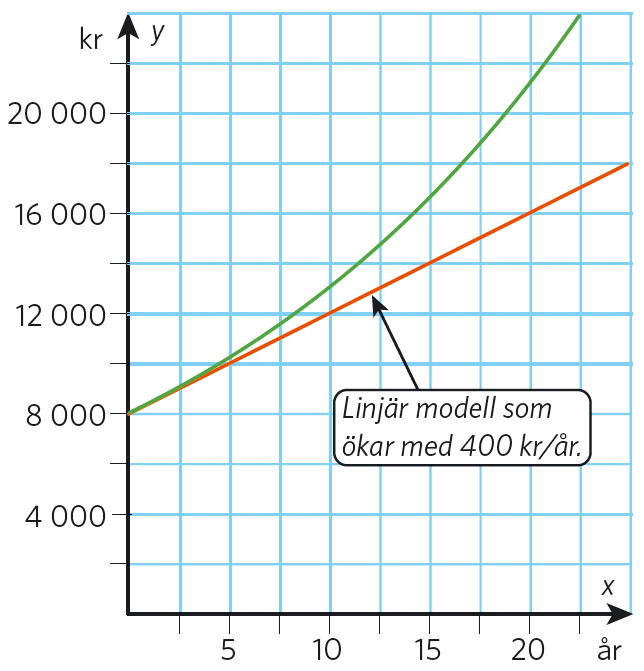
Gustav har #8\, 000 # kronor på sitt bankkonto. Beloppet växer med #5 # % varje år. Första året ökar Gustavs pengar med #5 # % av #8\, 000 # kr #= 400 # kr. Andra året har Gustav #8\, 400 # kr på kontot, och under året växer pengarna med #5 # % av #8\, 400 # kr #= 420 # kr. Ökningen är inte konstant. Det innebär att det inte går att använda en linjär modell.
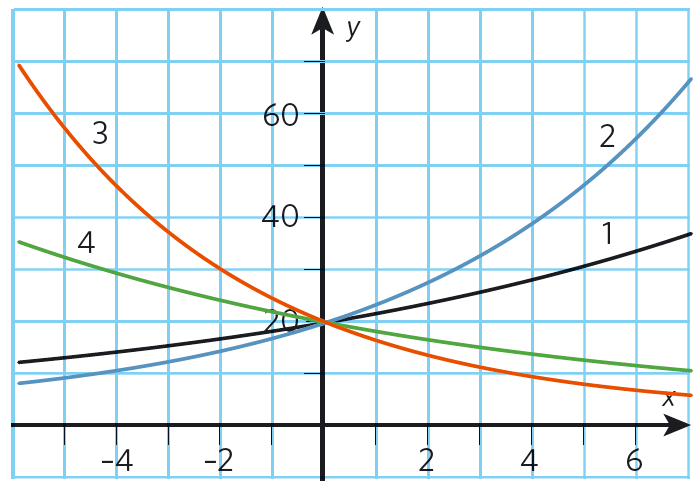
I figuren är #1 # och #2 # växande exponentialfunktioner, där förändringsfaktorn # a > 1#.
#3 # och #4 # är avtagande exponentialfunktioner, där förändringsfaktorn # a < 1#.
#\,#
Kontroll
Vilken eller vilka av funktionerna # a ( x ) # till # e ( x ) # här nedanför är
- växande exponentialfunktioner?
- avtagande exponentialfunktioner?
-
Hittar du någon funktion som inte är en exponentialfunktion? Vilken typ av funktion är det i så fall
#\begin{align*}
a(x) &= 500 \cdot 0{,}95^x &b(x) &= 200 + 45x \qquad c(x) = 900 \cdot 1{,}23^x \\ \\
d(x) &= 200 \cdot 0{,}1^x &e(x) &= 430 \cdot x^{1{,}{1}}
\end{align*}#
#\,#
Vi ställer upp en exponentialfunktion som visar hur Anitas pengar växer med tiden.
# y = 20\,000 \cdot a ^{ x }. #
Vi vet att # y (0) = 20\,000, # och # y (10) = 27\,405, # så #27\,405 = 20\,000 \cdot a ^{10}#.
#{a^{10}} = \frac{{27\,405}}{{20\,000}} \Rightarrow a = {\left( {\frac{{27\,405}}{{20\,000}}} \right)^{\tfrac{1}{10}}} \approx 1{,}032#
Anitas pengar växte alltså i genomsnitt med #3{,}2 # % per år!
Vi ställer upp en avtagande exponentialfunktion för hur antalet bakterier # N # beror av tiden # t#.
# N ( t ) = 1\,000\,000 \cdot 0{,}92^{ t } #
Efter #48 # h är antalet bakterier # N (48) = 1\,000\,000 \cdot 0{,}92^{48} \approx 18\,300 # st
#\,#
|
Exponentialfunktioner En exponentialfunktion kan skrivas på formen # y = C \cdot a ^{ x } # där # C # och # a # är konstanter. Förändringsfaktorn # a > 0#. Om # a > 1 # ökar funktionsvärdet # y # då # x # ökar. Funktionen är växande. Om #0 < a < 1 # minskar funktionsvärdet # y # då # x # ökar. Funktionen är avtagande. |