1c 4. Funktioner: 4.5 Grafisk ekvationslösning och modellering
Grafisk ekvationslösning
En del ekvationer är svåra att lösa exakt, och vissa är inte ens möjliga att lösa med en exakt metod. Då kan man använda sig av en grafisk lösningsmetod, där de reella lösningarna går att läsa ut ur en graf.
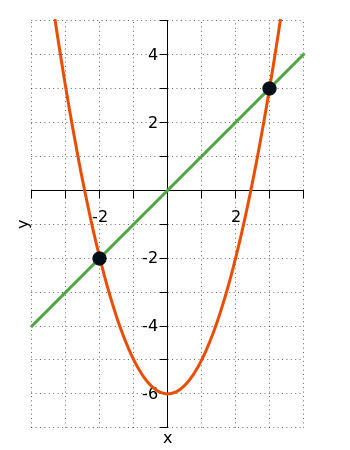
Lös ekvationen # x = x ^{2} - 6 # med en grafisk metod.
Lös ekvationen @2 * x ^{3,25} = 4 @ grafiskt.
Vi skapar en funktion av vänsterledet, och en av högerledet, och ritar båda på vår räknare.
Vi ställer in räknarens fönster så att #-10 < x < 10 # och #-10 < y < 10. # Det är standardinställningen på många räknare.
Grafernas skärningspunkt ligger där # x ≈ 1,24 # vilket vi får genom avläsning eller med hjälp av räknarfunktionen "intersect".
