Diskutera, resonera och modellera

1c 4. Funktioner: 4.5 Grafisk ekvationslösning och modellering

Diskutera, resonera och modellera

Acceleration Nivå 1

När vi löser problem med sträcka, hastighet och tid utgår vi ofta från att hastigheten är konstant, men så är det ju sällan i verkligheten. Ofta accelererar ett föremål så att dess hastighet ökar med tiden. Enheten för acceleration är m/s², som utläses meter per sekund per sekund, eller meter per sekund- kvadrat.

Vid fritt fall, det vill säga utan luftmotstånd, kan vi beräkna fallsträckan och hastigheten med hjälp av funktioner.

Fallsträcka: #s(t) = \frac{gt^2}{2}#

Hastighet: #v(t)=gt#

I båda funktionerna är #g# gravitationsaccelerationen, som i Sverige har värdet #g = 9,82# m/s².

#t# är tiden i sekunden, #s# är i m och #v# i m/s.

Gör en tabell som visar hur långt man faller på #0#, #1#, #2#, #3#, #4# och #5# sekunder, och vilken hastighet man har vid dessa tidpunkter.
Gör en graf som visar hur hastigheten varierar med tiden.
Gör en graf som visar hur fallsträckan varierar med tiden.
Vilken medelhastighet har man om man fallit fritt i #5# sekunder? Hur kan du illustrera medelhastigheten i din graf som visar hastigheten som funktion av tiden?
Visa att arean under grafen i ditt hastighet-tid-diagram har samma värde som fallsträckan.

#\,#

Svar

#\,#

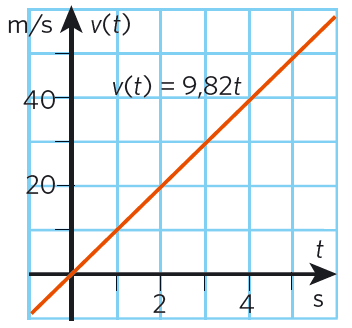
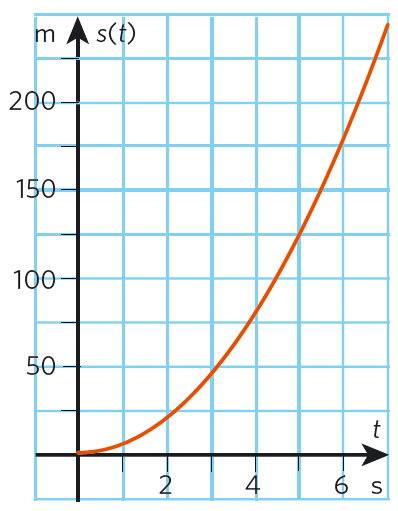
#t# (s) #s(t)# (m) #v(t)# (m/s)

#0# #0# #0#

#1# @4,91@ @9,82@

@2@ @19,64@ @19,64@

@3@ @44,19@ @29,46@

@4@ @78,56@ @39,28@

@5@ @122,75@ @49,1@
#\,#
#\,#
Medelhastigheten är

@(v(5)+v(0))/2 = (49,1+0)/2@ m/s @= 24,55@ m/s

I en proportionalitet, t.ex. @v(t) = 9,82t@, hittar vi medelvärdet av två funktionsvärden genom att titta på funktionsvärdet för det @t@ som ligger precis mitt emellan @t@-värdena för de två funktionsvärden för vilka vi vill beräkna medelvärdet.

I det här fallet är alltså medelvärdet av @v(5)@ och @v(0)@. @(v(0)+v(5))/2=v(2,5)@

Mitt emellan @t=0@ och @t=5@ ligger @t=2,5@.
#\,#

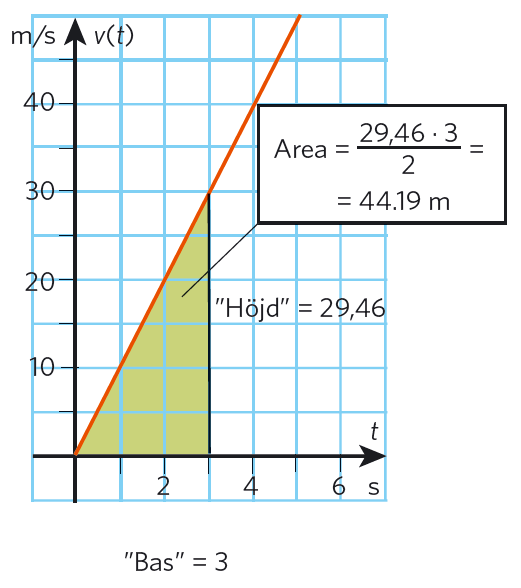
Arean under grafen är en triangel, så vi börar med att bestämma bas och höjd.

Om vi vill veta arean mellan @t=0@ och @t=3@ mäter vi @3@ enheter längs @t@-axeln. Det är triangelns bas.

Höjden är funktionsvärdet. @v(3)=29,46@ i figuren.

Triangelns area blir då@(3*29,46)/2=44,19@

Vi vill veta sträckan efter @t@ sekunder. Triangeln har basen @t@ och höjden blir @v(t)@.

Arean blir @(t*v(t))/2 = (t*9,82t)/2 = (9,82t^2)/2@

Dvs. samma uttryck som fallsträckan!

#\,#

Acceleration Nivå 2

Om till exempel en bil eller en boll har konstant acceleration (fartökning per tidsenhet) beräknas sträckan #s# vid tiden #t# som

#\qqqquad s(t) = v_0t + \frac{at^2}{2}#

Hastigheten vid tidpunkten #t# beräknas som

#\qqqquad s(t) = v_0 + at#

Här är #v_0# vår starthastighet i m/s, och #a# är accelerationen i m/s².

Karin kör med hastigheten #15# m/s när hon accelerar med #2# m/s² i #5# sekunder.

Gör en tabell som visar hur Karins hastighet beror av tiden.
Rita ett hastighet-tid-diagram som visar hur hastigheten beror av tiden.
Vilken hastighet har Karin efter accelerationen?
Hur långt har Karin kört på fem sekunder, och vilken är hennes medelhastighet?

Nedanför ser du ett hastighet-tid-diagram för en boll som rullar i en nedförsbacke.

Vilken starthastighet har bollen?
Vilken hastighet har bollen efter #7# sekunder?
Vilken medelhastighet har bollen under de första #10# sekunderna?
Vilken acceleration har bollen?
Hur lång sträcka rullar bollen under #10# sekunder?

#\,#

Svar - Karin

#\,#

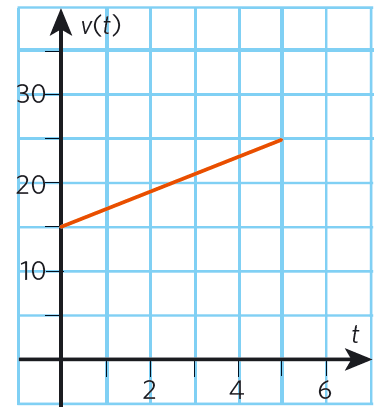
#t# #v(t)#

@0@ @15@

@1@ @17@

@2@ @19@

@3@ @21@

@4@ @23@

@5@ @25@
#\,#
Vid tiden #t=5# s har Karin hastigheten @25@ m/s.
@s(5)@=(15*5+(2*5^2)/2)@ m @= 100@ m

Karin kör @100@ m på @5@ sekunder. Hennes medelhastighet är @100/5@ m/s @=20@ m/s.

#\,#

Svar - bollen

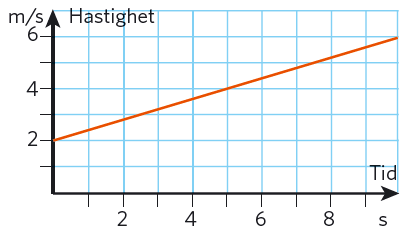
och b. Bollen startar med @2@ m/s, och efter @7@ sekunder har den hastigheten @4,8@ m/s.

Efter @10@ sekunder har bollen hastigheten @(2+0,4*10)@ m/s @= 6@ m/s. Medelhastigheten under de första @10@ sekunderna är

@(v(0)+v(10))/2 = (2+6)/2@ m/s @=4@ m/s

Värdena kan också utläsas ur diagrammet.
Linjens lutning är accelerationen, @0,4@ m/s².
Under @10@ s hinner bollen @(4*10)@ m @= 40@ m.

#t# (s)	#s(t)# (m)	#v(t)# (m/s)
#0#	#0#	#0#
#1#	@4,91@	@9,82@
@2@	@19,64@	@19,64@
@3@	@44,19@	@29,46@
@4@	@78,56@	@39,28@
@5@	@122,75@	@49,1@

#t#	#v(t)#
@0@	@15@
@1@	@17@
@2@	@19@
@3@	@21@
@4@	@23@
@5@	@25@