|
Fixpunktsiteration Nivå 2
Vi har tittat på hur man kan lösa ekvationer grafiskt. Här ska vi arbeta med en annan metod som inte kräver något grafiskt hjälpmedel. Den kan kännas lite omständlig, men används ofta när man har en dator till hjälp för beräkningar.
Vi vill lösa ekvationen #x=1+\sqrt x#.
Om vi låter #x=2# blir högerledet #1+\sqrt 2 \approx 2,4142#, vilket är för stort. Om vi låter #x=3# blir högerledet #1+\sqrt 3 \approx 2,7321#, vilket är för litet. Någonstans mellan #x=2# och #x=3# ligger alltså vår lösning.
Metoden vi ska använda oss av kallas för fixpunktsiteration.
Vi utgår från en ekvation som har utseendet #x=f(x)# och väljer ett #x#-värde att börja med. Därefter beräknar vi högerledets värde för vårt valda #x#-värde. Resultatet från beräkningen använder vi sedan som vårt nya #x#-värde, beräknar högerledet för det nya #x#-värdet, och så upprepar vi processen tills vi är klara.
Om vi söker en lösning med tre decimalers noggrannhet är vi klara när den fjärde decimalen inte längre förändras. Först då vet vi att avrundningen till tre decimaler blir korrekt. Bilden nedan visar hur fixpunktsiteration går till grafiskt.
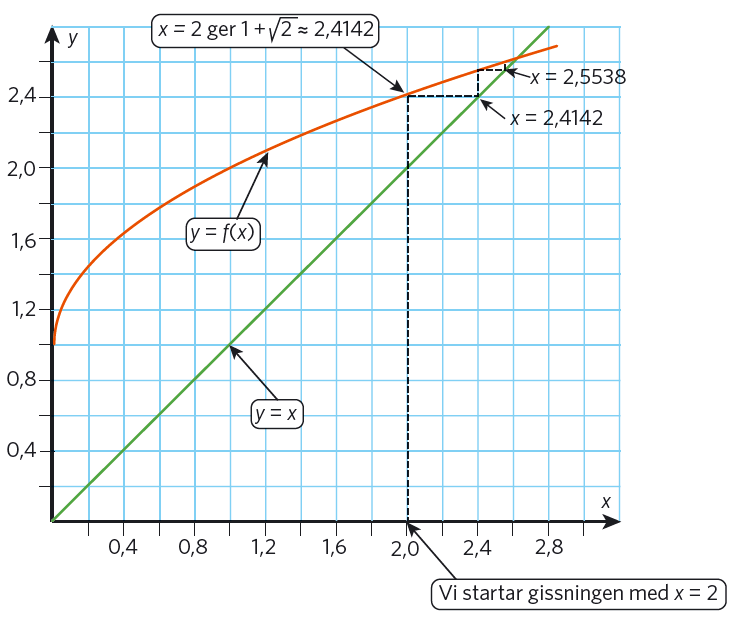
Här söker vi ett närmevärde med tre decimaler till ekvationen #x=1+ \sqrt x#:
#x=2# ger ett närmevärde på #1+\sqrt{2} \approx 2{,}4142#
#x=2{,}4142# ger ett närmevärde på #1+\sqrt{2{,}4142} \approx 2{,}5538#
#x=2{,}5538# ger ett närmevärde på #1+\sqrt{2{,}5538} \approx 2{,}5981#
#x=2{,}5981# ger ett närmevärde på #1+\sqrt{2{,}5981} \approx 2{,}6119#
#x=2{,}6119# ger ett närmevärde på #1+\sqrt{2{,}6119} \approx 2{,}6161#
#x=2{,}6161# ger ett närmevärde på #1+\sqrt{2{,}6161} \approx 2{,}6174#
#x=2{,}6174# ger ett närmevärde på #1+\sqrt{2{,}6174} \approx 2{,}6178#
#x=2{,}6178# ger ett närmevärde på #1+\sqrt{2{,}6178} \approx 2{,}6180#
#x=2{,}6180# ger ett närmevärde på #1+\sqrt{2{,}6180} \approx 2{,}6180#
Här överensstämmer vänster- och högerleden ungefär, och vi har hittat en lösning: #x \approx 2,618#. Observera att det tog #9# beräkningssteg. Ju närmare lösningen vi startar, desto färre beräkningar behöver vi göra.
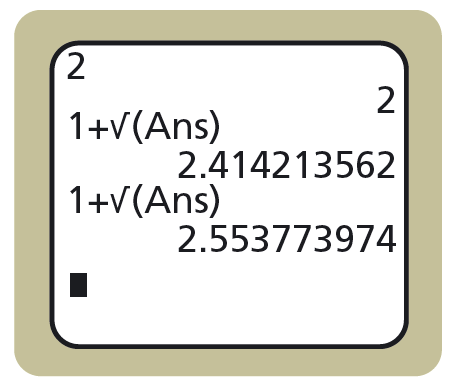
Med en modern räknare kan vi effektivisera beräkningen genom att använda räknarens svarsfunktion (ANS). Testa hur du kan använda din räknare till detta.
På vissa räknare kan man börja genom att skriva #2# <ENTER>.
Därefter skriver man funktionen, men byter ut #x# mot ANS:
#1+\sqrt{\rm{ANS}}# <ENTER>
Många räknare har möjligheten att ta fram det man senast skrev in (på vissa räknare är det "2nd" följt av "ENTER"). Det kan man använda för att snabbt göra alla sina beräkningssteg, eftersom räknaren använder det senaste svaret i den nya beräkningen precis som iterationsmetoden ska göra.
Ett bättre sätt att presentera lösningen är i tabellform:
| #x# |
#a# |
| #2# |
#2{,}4142# |
| #2{,}4142# |
#2{,}5538# |
| #2{,}5538# |
#2{,}5981# |
| #2{,}5981# |
#2{,}6119# |
| #2{,}6119# |
#2{,}6161# |
| #2{,}6161# |
#2{,}6174# |
| #2{,}6174# |
#2{,}6178# |
| #2{,}6178# |
#2{,}6180# |
| #2{,}6180# |
#2{,}6180# |
|
|
#\,#
#\,#
#\,#
#\,#
#\,#
#\,#
#\,#
Om vi nöjer oss med två decimalers noggranhet kan vi sluta iterationen här
|
|
#\,#
Använd fixpunktsiteration för att hitta lösningar med #3# decimalers noggrannhet till ekvationerna nedan. Börja med att hitta ett tal som är nära lösningen. Redovisa uträkningar för varje steg, eller i tabellform.
- #x=4+\sqrt x#
- #x= \frac{4}{\sqrt{x+1}}#
- #x-1=\frac{8}{\sqrt{x^3}}#
I c-uppgiften får du vara beredd på att göra många beräkningssteg!
Rita graferna till #y=x-1# och #y=\frac{8}{\sqrt{x^3}}# och fundera över varför det krävs så många steg för att komma fram till en noggrann lösning.
|
|
 Diskutera, resonera och modellera
Diskutera, resonera och modellera



