|

#\,#
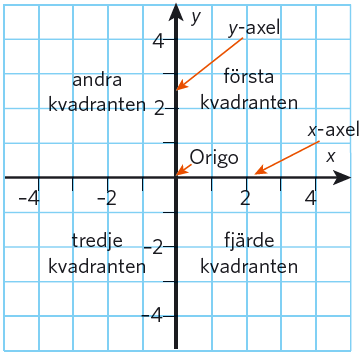
Koordinatsystem
|
#\,#
Definitionsmängd och värdemängd
De tillåtna # x #-värdena för en funktion kallas funktionens definitionsmängd.
De # y #-värden som svarar mot de tillåtna # x #-värdena kallas funktionens värdemängd.
|
#\,#
|
#\,#
#\,#
Funktioner
En funktion är ett samband mellan beroende och oberoende variabler.
En funktion beskriver ofta ett skeende.
# y # är en funktion av # x # om det för varje värde på # x # finns endast ett värde på # y#.
|
#\,#
#\,#
Proportionalitet
Direkt proportionalitet: # y = kx #
Proportionalitetskonstant: #k = \frac{{y{\text{-värdet}}}}{{x{\text{-värdet}}}}#
Proportionalitetskonstanten, "k-värdet", är ett mått på linjens lutning i förhållande till # x #-axeln.
Grafen till en direkt proportionalitet är en rät linje som alltid går genom origo.
|
#\,#
#\,#
#\,#
#\,#
|
|
#\,#
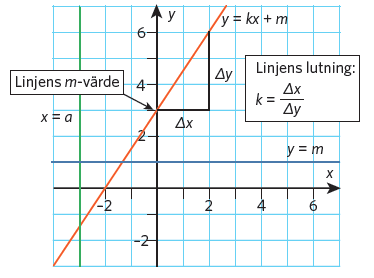
Räta linjer
Räta linjens ekvation på #k#-form: #y=kx+m#
Ett positivt #k#-värde innebär att #y#-värdet ökar då #x# ökar.
Ett negativt #k#-värde innebär att #y#-värdet minskar då #x# ökar.
Parallella linjer har samma riktning och därmed samma #k#-värde.
Linjen #y = m# är parallell med #x#-axeln
Linjen #x = a# är parallell med #y#-axeln
|
|
#\,#
Potensfunktioner
Funktioner av typen # f ( x ) = C \cdot x ^{ n }, # där # C # och # n # är konstanter, är potensfunktioner.
|
#\,#
#\,#
Exponentialfunktioner
En exponentialfunktion skrivs på formen # y = C \cdot a^x#, där # C # och # a # är konstanter. # C # är startvärdet för funktionen, # a # är förändringsfaktorn. # a > 0#.
Om # a > 1 # och # C > 0 # ökar funktionsvärdet # y # då # x # ökar. Funktionen är växande.
Om #0 < a < 1 # och # C > 0 # minskar funktionsvärdet # y # då # x # ökar. Funktionen är avtagande.
|
|
|
Olika former av räta linjens ekvation
#y=kx+m#
#y=k(x-x_1) + y_1#
#ax+by + c = 0#
#k#-form
enpunktsform
allmän form
|
#\,#
Vinkelräta linjer
Två räta linjer med riktningskoefficienterna # k _{1} # och # k _{2} # är vinkelräta mot varandra om # k _{1} \cdot k _{2} = -1 #
En linje som är vinkelrät mot en annan kallas ofta för en normal.
#y_{1} # ⊥ # y _{2} # betyder att linjerna # y _{1} # och # y _{2} # är vinkelräta mot varandra.
|
#\,#
|
|
|
|
|
|
|
|

