1c 4. Funktioner: 4.2 Funktioner i matematiken
 Funktioner i matematiken
Funktioner i matematiken
Ordet funktion används i många sammanhang. Det kan handla om sådant som fungerar eller inte fungerar i samhället, i våra kroppar eller i tekniska prylar. Även i matematiken är funktion ett vanligt och viktigt begrepp, men i matematiken har ordet funktion en lite annan innebörd än i vardagsspråket.
Det är inte helt lätt att beskriva vad som menas med en matematisk funktion. Ofta används ord som samband eller regel. Yrkesmatematiker definierar en funktion som en avbildning. Funktioner i matematik kan också se ut på väldigt många olika sätt. Ibland är de tydligt knutna till förhållanden i verkligheten, ibland är de rent abstrakta. De funktioner vi kommer att möta i gymnasiematematiken kan ofta ses som något slags utveckling, skeenden, eller förlopp. Ofta blir begrepp tydligare med exempel. Vi börjar med ett enkelt sådant.
En funktion som beskriver ett förlopp
Från mynningen av ett rör, ett stycke över marken, rinner vatten med jämt flöde. Vid en tidpunkt som vi kallar noll ställer vi en tom, tjugo centimeter hög, cylinderformad burk under rörmynningen. Efter precis tio sekunder är burken full med vatten.
Hur vattnets höjd i burken går från noll till tjugo centimeter är ett förlopp som vi kan beskriva med en enkel matematisk funktion. Vi ger funktionen namnet #f#. Tiden från tidpunkten noll, mätt i sekunder, betecknar vi med #t#. Vattnets höjd i burken, mätt i centimeter, får då beteckningen #f(t)#. Att denna beteckning innehåller ett #t# inom parentes, är ett sätt att visa att vattnets höjd i burken #f(t)#, är beroende av hur lång tid, #t#, som gått sedan tiden #0#. I matematiken brukar man uttrycka det som att #f(t)# beror av #t#.
Värdetabell
Eftersom vattenflödet är konstant, kan vi dra slutsatser om vattnets höjd vid olika tidpunkter och ställa upp en värdetabell.
| #t# | #f(t)# |
| #0# | #0# |
| #2# | #4# |
| #4# | #8# |
| #6# | #12# |
| #8# | #16# |
| #10# | #20# |
Med beteckningarna #t# och #f(t)# kan vi också uttrycka värdena som #f(0)=0#, #f(2)=4#, och så vidare. Detta utläses ”f av noll är noll”, ”f av två är fyra”, ... Naturligtvis hade vi även kunnat ta med andra värden i tabellen, exempelvis #f(3)=6# och #f(5,5)=11#. Eftersom värdena på #t# och #f(t)# kan variera, kallas #t# och #f(t)# för variabler. #t# är den oberoende variabeln och #f(t)# är den beroende variabeln.
Graf
Funktionen #f# beskriver ett förlopp, eller ett samband. Tabellen är ett sätt att visa hur detta samband ser ut. Tabellen är ett sätt att representera funktionen. Ett annat sätt att representera funktionen är med ett diagram.
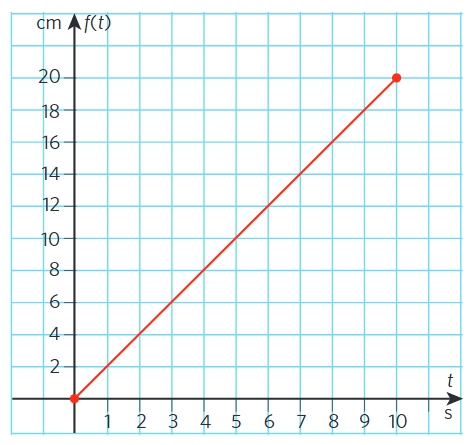
Den horisontella axeln visar tiden och den lodräta visar vattenhöjden. Varje punkt på den raka, röda kurvan visar vattnets höjd i burken vid någon bestämd tidpunkt. Mängden av alla punkter som visas på kurvan kallas funktionens graf. Ofta säger man lite förenklat att själva kurvan är grafen.
Ekvation
Ett tredje sätt att representera en funktion, är genom en ekvation. Från beskrivningen av förloppet, tabellen och grafen, kan vi dra slutsatsen att funktionen #f# kan beskrivas med ekvationen \[ f(t)=2t \qquad(0\leq t\leq10) \] Det är viktigt att ha med uttrycket #0\leq t\leq10#, eftersom funktionen endast är definierad (giltig) för dessa värden på #t#. #0\leq t\leq10# kallas funktionens definitionsmängd. Hade inte definitionsmängden angetts, skulle det tolkats som att funktionen var definierad för alla värden på #t#, vilket inte stämmer i detta fall.
Vattnets höjd i cm i hinken kan anta alla värden mellan #0# och #20#. Vi säger att funktionens värdemängd är #0\leq f(t) \leq 20#.
Mängden av alla värden på #t# för vilka funktionen är definierad kallas definitionsmängden för #f#.
Mängden av alla värden #f(t)# kan anta kallas värdemängden för #f#.
När man utgår från en ekvation för att beskriva en funktion, säger man att ekvationen definierar eller bestämmer funktionen.
Beteckningar
#t# är en vanlig beteckning för den oberoende variabeln om den representerar tid. I mer allmänna sammanhang betecknas den oberoende variabeln ofta #x#. Om funktionen är #f# betecknas den beroende variabeln då #f(x)#.
Inte heller har alla funktioner namnet #f#. Särskilt när man arbetar med flera olika funktioner samtidigt måste man kunna variera. Andra vanliga namn är exempelvis #g#, #h# och #f_1, f_2,f_3, \ldots#
Den beroende variabeln i en funktion kan också betecknas med det neutrala #y#. Detta har att göra med att då grafen av en funktion återges i ett koordinatsystem, visas den oberoende variabeln på #x#-axeln och den beroende variabeln på #y#-axeln.
- Vilken är den oberoende variabeln i funktionen?
- Vilken är den beroende variabeln?
- Vilken är definitionsmängden?
- Ange värdemängden.

