1c 4. Funktioner: 4.2 Funktioner i matematiken
 Mer om funktioner
Mer om funktioner
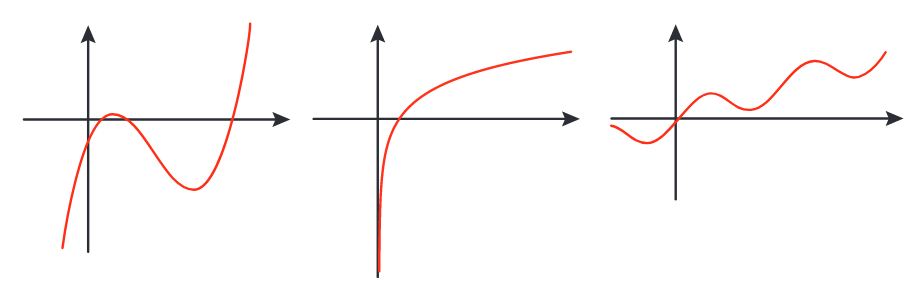
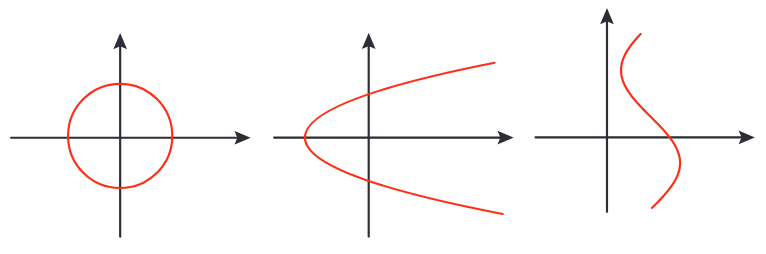
Graferna till funktionerna i det föregående avsnittet bestod alla av räta linjer eller delar av sådana. Så behöver det inte vara. Kurvorna i figurena i exemplet nedan kan alla tre vara grafer till funktioner.
Funktionen #f# har en graf som i figuren nedan.
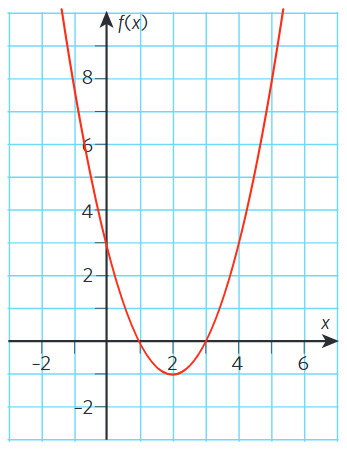
En värdetabell för #f# kan vara
| #t# | #f(t)# |
| #-1# | #8# |
| #0# | #3# |
| #1# | #0# |
| #2# | #-1# |
| #3# | #0# |
| #4# | #3# |
| #5# | #8# |
Vi ser att #f(1)=0# och #f(3)=0#. Vi säger att #x=1# och #x=3# är nollställen till funktionen #f#.
Vi ser också att olika värden på den oberoende variabeln #x# kan ge samma värden på den beroende variabeln #f(x)#. Så är det för de två nollställena, men exempelvis också för #f(-1)=f(5)=8#. Detta är fullt tillåtet och utgör inget problem i en funktion. Däremot måste varje värde i definitionsmängden svara mot precis ett värde i värdemängden. I exemplet måste det för varje tillåtet värde på #x# alltså finnas precis ett värde på #f(x)#. För en kurva som visar grafen till en funktion, kan två eller flera punkter därför aldrig ligga på samma lodräta linje.
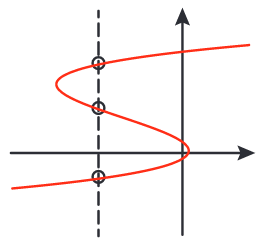
Kurvan i figuren nedan skär samma lodräta linje tre gånger. En sådan kurva kan aldrig var en graf till en funktion.
Vi söker funktionens värde för # x = 1. # Alltså läser vi av # y #-koordinaten för den punkt på grafen där # x = 1. #
# f (1) = -4 \qqqquad#Funktionens värde är #-4 # för # x = 1#.