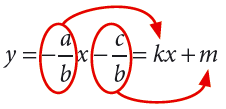Enpunktsform

Ekvationen för en rät linje kan bestämmas på flera olika sätt. Om du känner till koordinaterna för en punkt samt linjens lutning kan du använda dig av den så kallade enpunktsformen. Vi kallar koordinaterna för den kända punkten för #( x _{1}, y _{1}). # En annan godtycklig punkt på linjen har koordinaterna #( x , y )#.

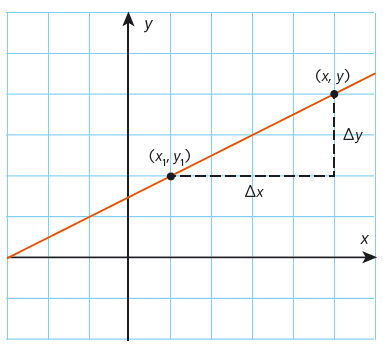
För att bestämma linjens lutning # k # använder vi sambandet #k = \frac{{\Delta y}}{{\Delta x}} = \frac{{y - {y_1}}}{{x - {x_1}}}#.

Ur sambandet löser vi ut # y # genom att multiplicera båda sidor med nämnaren # x - x _{1}#.

#k = \frac{{y - {y_1}}}{{x - {x_1}}}# ⇔ # k ( x - x _{1}) = y - y _{1} #

Därefter adderar vi # y _{1} # till båda leden och får

# k ( x - x _{1}) + y _{1} = y # eller

# y = k ( x - x _{1}) + y _{1} #

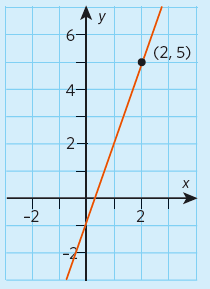
Vi använder enpunktsformen # y = k ( x - x _{1}) + y _{1} # där #( x _{1}, y _{1}) = (2, 5) # och # k = 3#.

# y = 3( x - 2) + 5 = 3 x - 6 + 5 = 3 x - 1 # Linjen # y = 3 x - 1 # uppfyller villkoren.

Nästa exempel

Allmän form

Den allmänna formen förekommer ofta när vi arbetar med digitala verktyg.

Räta linjens ekvation på allmän form är # ax + by + c = 0#.

Genom att lösa ut # y # får vi linjens ekvation på # k #-form:

Linjen har alltså lutningen #k = - \frac{a}{b}#, och y-koordinaten för skärningspunkten med # y #-axeln är #m = - \frac{c}{b}#.