Vinkelräta linjer

1c 4. Funktioner: 4.3 Linjära samband

Vinkelräta linjer

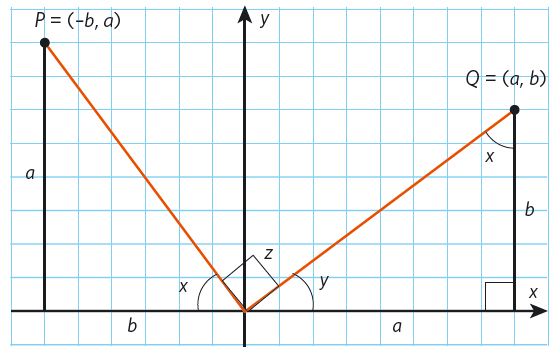
I figuren nedan har vi ritat två räta linjer som utgår från origo och slutar i var sin ändpunkt, # P # respektive # Q#. Hur stor är vinkeln mellan linjerna?

Vi drar räta linjer från punkterna rakt ner mot # x #-axeln. Då bildas två rätvinkliga trianglar. Sidornas längder bestäms av koordinaterna för punkterna. Vi ser att trianglarna är kongruenta. Det betyder att de har precis lika långa sidor, och att alla vinklar i den ena triangeln är precis lika stora som motsvarande vinklar i den andra triangeln.

Vinkeln #x + y+ z = 180°#. I en rätvinklig triangel gäller # x + y + 90° = 180°\text{.}# Det innebär att vinkeln # z = 90°# och att linjerna # OP # och # OQ # alltså bildar rät vinkel med varandra. Ofta skriver man # OP \perp OQ#. En linje som är vinkelrät mot en annan rät linje kallas ofta för en normal.

^{Symbolen #\perp#betyder att en linje är vinkelrät mot en annan.}

Linjen # OP # har lutningen #{k_1} = \frac{{\Delta y}}{{\Delta x}} = \frac{{0 - a}}{{0 - ( - b)}} = - \frac{a}{b}#

Linjen # OQ # har lutningen #{k_2} = \frac{{\Delta y}}{{\Delta x}} = \frac{{b - 0}}{{a - 0}} = \frac{b}{a}#

Produkten mellan lutningarna för linjerna är #{k_1}{k_2} = - \frac{a}{b} \cdot \frac{b}{a} = - 1#

Vinkelräta linjer

Två räta linjer med riktningskoefficienterna # k _{1} # och # k _{2} # är vinkelräta mot varandra om # k _{1} \cdot k _{2} = -1 #

En linje som är vinkelrät mot en annan kallas ofta för en normal.
# y _{1} \perp y _{2} # betyder att linjerna # y _{1} # och # y _{2} # är vinkelräta mot varandra.

#\,#

Kontroll

Vilken lutning har en linje som är vinkelrät mot # y = 4 x + 7#?

Svar

#k = -0{,}25#

#\,#

Bestäm ekvationen för en linje som är vinkelrät mot linjen # y = 5 x - 11#.

Den sökta linjen har lutningen # k . # Produkten mellan riktningskoefficienterna ska vara #-1#:

#5 \cdot k = -1 ⇔ k = - \frac{1}{5}#

Normalen till # y = 5 x - 11 # är då till exempel #{y_ \perp } = - \frac{x}{5}#.

^{Kom ihåg: #x \cdot \frac{1}{a} = \frac{x}{a}#}

Nästa exempel

Vilken ekvation har linjen som är vinkelrät mot # y = -2 x + 4 # och som går genom punkten #(3, 11)#?

Den sökta vinkelräta linjen har ekvationen # y _\perp= k _\perp x + m #

Produkten mellan lutningarna är #-1#:

#-2 \cdot k_ \bot= -1 ⇔ {k_ \bot } = \frac{{ - 1}}{{ - 2}} = 0,5#

Det innebär att # y_ \perp= 0{,}5 x + m#. Vi sätter in punkten #(3, 11) # och bestämmer # m #:

#11 = 0,5 \cdot 3 + m # ⇔ # m = 11 - 1,5 = 9{,}5 #

Den sökta linjens ekvation är # y_ \perp= 0,5 x + 9,5#.

Nästa exempel

Utanför linjen # y = 0,5 x + 2 # ligger punkten # P = (3, 1)#. Bestäm koordinaterna för punkten # P'# som är speglingen av punkten # P # i linjen.

Med speglingen # P'# menar vi en punkt som ligger lika långt från linjen som punkten # P#, och där både # P # och # P'# ligger på en linje som är vinkelrät mot den kända linjen.

Den linje som både # P # och # P'# ligger på har riktningskoefficienten #-2#, eftersom #-2 \cdot 0,5 = -1#.

Den vinkelräta linjens ekvation: # y_ \perp = -2 x + m #

En punkt på linjen är # P = (3, 1)#. Vi sätter in punkten i den vinkelräta linjens ekvation:

#1 = -2 \cdot 3 + m #

# m = 7 #

Den vinkelräta linjen (normalen) till linjen # y = 0,5 x + 1 # är # y_\perp= -2 x + 7#.

För att kunna bestämma avståndet mellan punkten # P # och linjen bestämmer vi nu skärningspunkten mellan de båda räta linjerna. I skärningspunkten gäller

#0{,}5 x + 1 = -2 x + 7 \qquad \text{(}y\text{-koordinaterna lika)}#

#2{,}5 x = 6 #

# x = 2{,}4 #

Att # x = 2{,}4 # ger # y = 0,5 \cdot 2{,}4 + 1 = 2{,}2 #

Skärningspunkten har koordinaterna #(2{,}4; 2{,}2) #

För att gå från # P = (3, 1) # till skärningspunkten behöver vi förflytta oss # \Delta x = 0{,}6 # i negativ # x #-riktning och #\Delta y = 1{,}2 # i positiv # y #-riktning.

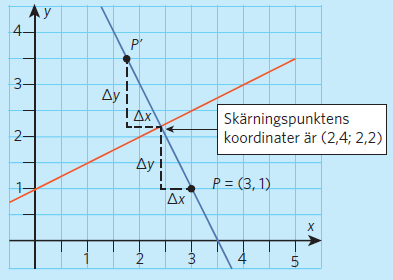
Spegelpunkten # P'# kommer vi till om vi går lika långt och på samma sätt från skärningspunkten. Vi tar #0{,}6 # steg i negativ # x #-riktning och #1,2 # steg i positiv # y #-riktning:

Från # x = 2,4 # går vi #-0,6 # steg till # x = 1,8 #

Från # y = 2,2 # går vi #1,2 # steg till # y = 3,4 #

# P'# har koordinaterna #(1{,}8; 3{,}4)#.

Nästa exempel