|
Passare och linjal – Geometri i GeoGebra
Traditionen att konstruera geometriska objekt med endast passare och linjal började i det antika Grekland. En av de mest kända matematikerna vid den tiden var Euklides. Euklides lade grunden till den geometri som vi idag använder. Han formulerade axiom (efter grekiskans axioma som betyder värdering), eller postulat. Euklides första axiom eller postulat lyder till exempel "Genom två olika punkter går precis en rät linje". Särskilt känt är det femte postulatet, som indirekt handlar om parallella linjer och därför ofta kallas parallellaxiomet. Det går att skapa geometriska system utan parallellaxiomet, men i sådana system ser samband och räkneregler annorlunda ut.
Euklides tredje postulat lyder "En cirkel kan uppritas med godtyckligt centrum och godtycklig radie". Cirklar används bland annat för att konstruera räta vinklar och för att dela sträckor i två lika delar. Verktyget för att rita cirklar var passare. Så sent som i slutet av 1800-talet var ledande matematiker sysselsatta med att visa vad som kunde skapas med passare och linjal.
I denna datorövning konstruerar vi räta vinklar genom att använda GeoGebras verktyg för att rita räta linjer, sätta ut punkter och skapa cirklar, det vill säga digitala motsvarigheter till just passare och linjal. Vi har utgått ifrån GeoGebra desktop 5.0 svensk. Detaljer kan skilja i andra versioner.
Verktyg i GeoGebra
Gå igenom tabellen och kontrollera att du kan hitta alla dessa verktyg i programmet.
| Cirkel |
 |
|
| Punkt |
 |
|
| Flytta |
 |
|
| Skärning mellan två objekt |
 |
|
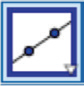
| Linje |
 |
|
| Sträcka |
 |
|
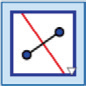
| Mittpunktsnormal |
 |
|
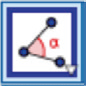
| Vinkel |
 |
|
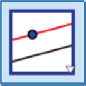
| Parallell linje |
 |
|
| Vinkelrät linje |
 |
|
| Polygon |
 |
|
| Visa/dölj |
 |
|
#\,#
Del I - konstruera en normal
En linje som är vinkelrät mot en given rät linje kallas normal till den givna linjen. GeoGebra har ett speciellt verktyg för att ta fram en normal, men det ska vi inte använda. I stället följer vi den klassiska metoden.
- Öppna ett nytt fönster i GeoGebra.
- Högerklicka i ritområdet. Avmarkera "Visa axlar och Rutnät".
- Välj Visa. Avmarkera Algebrafönster och Inmatningsfält.
- Välj Inställningar - Namn på objekt - Endast nya punkter
- Rita en linje genom två punkter A och B, med hjälp av linjeverktyget.
- Välj cirkelverktyget. Klicka först på punkten A och sedan på linjen AB någonstans närmare B än A. En cirkel med medelpunkt A ska synas, dess skärningspunkt med linjen AB ska ha beteckningen C.
- Rita på motsvarande sätt en cirkel vars medelpunkt är B och vars skärning med linjen AB ligger närmare A än B. Den nya cirkelns skärningspunkt med linjen AB ska ha beteckningen D.
- Välj verktyget Skärning mellan två objekt (under verktyget för Punkt), klicka sedan på den ena cirkeln och sist på den andra. Skärningspunkterna mellan cirklarna ska nu vara markerade som E och F.
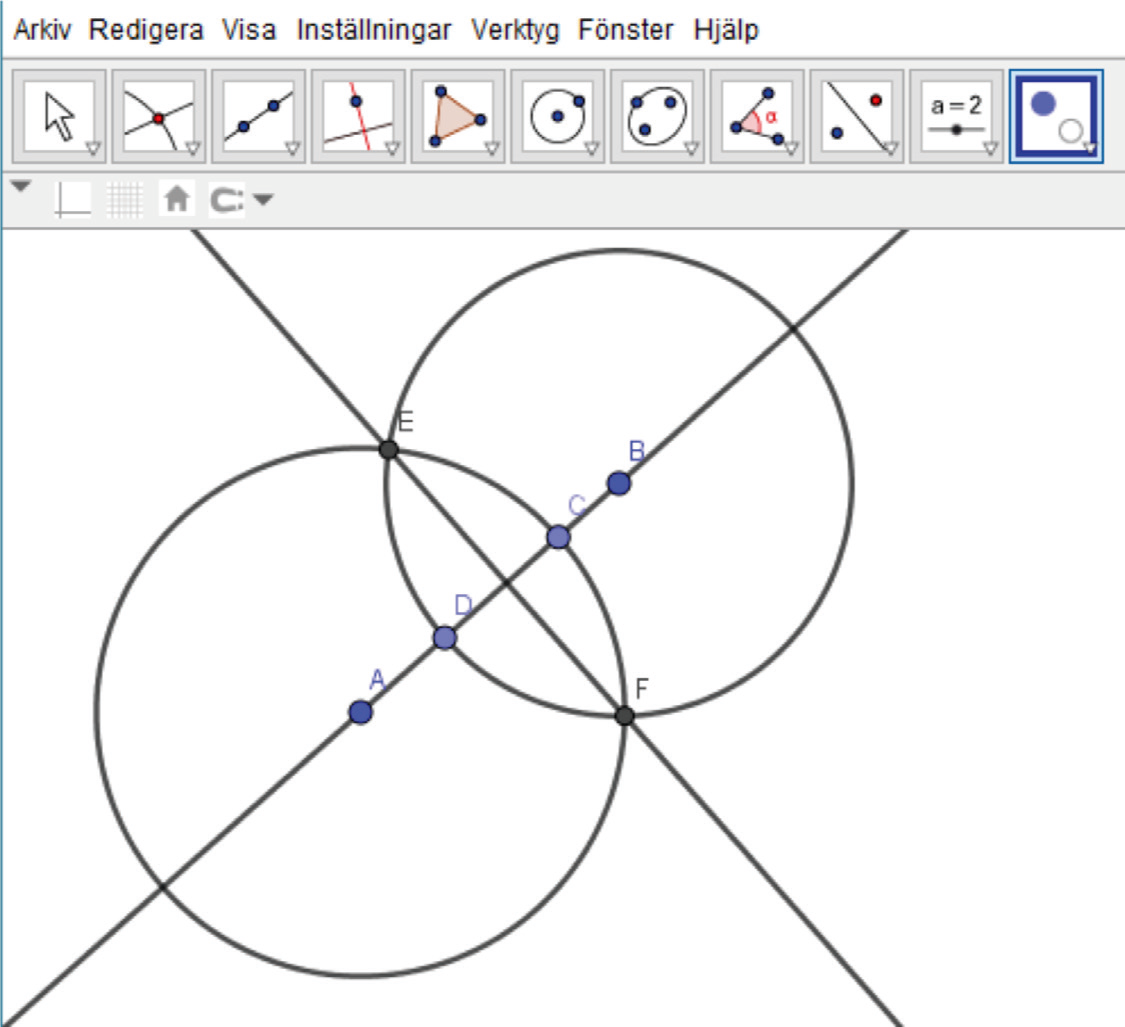
- Välj verktyget Linje, klicka sedan på punkten E och sedan på punkten F. Linjen EF ser ut att vara vinkelrät mot AB. Vi ska undersöka om detta verkligen stämmer.
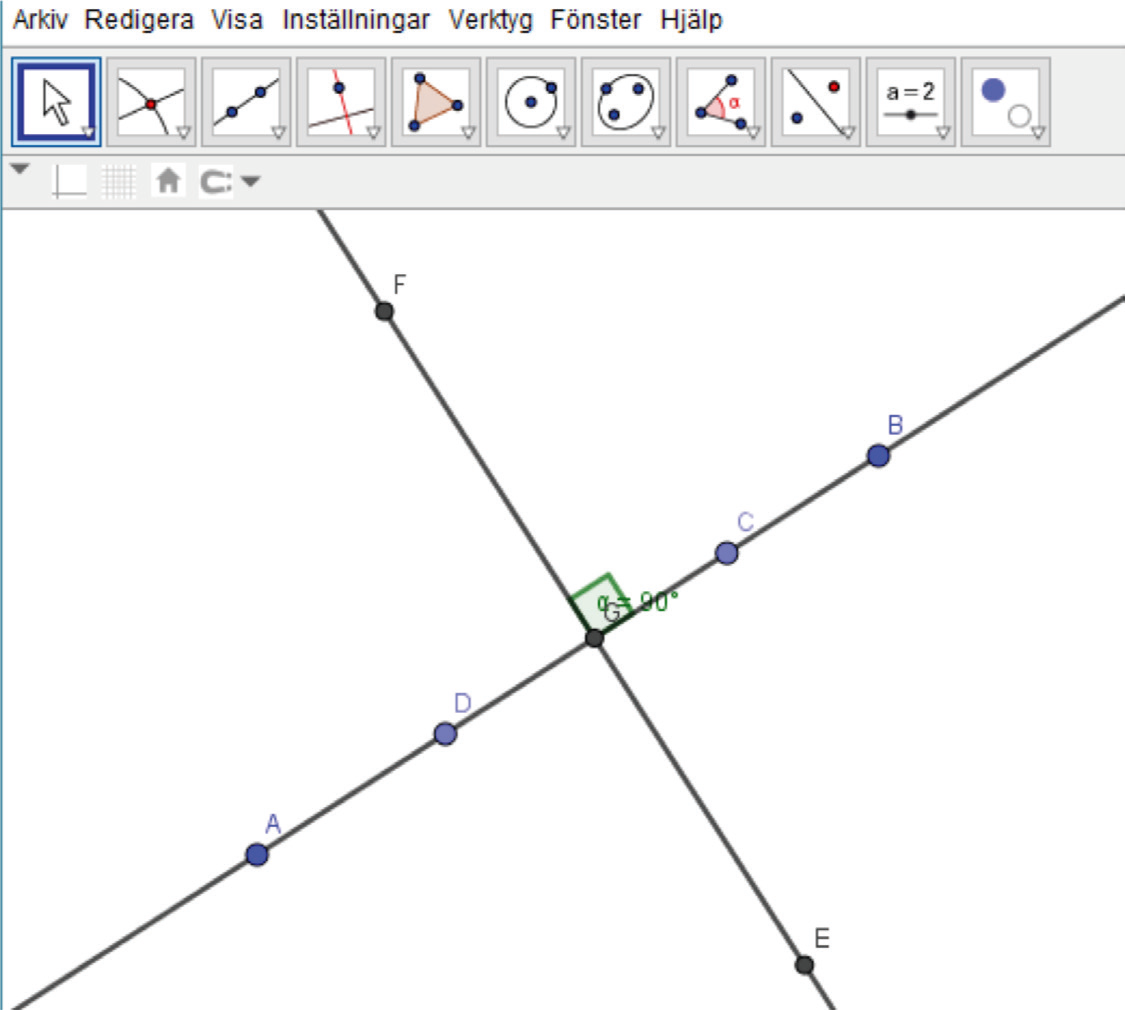
- Välj åter verktyget Skärning mellan två objekt, sedan linjen AB och sist linjen EF. Skärningspunkten mellan linjerna ska vara markerad som G.
- Välj verktyget vinkel och sedan antingen punkterna C, G och F, eller punkterna C, G och E. I något av fallen ska en markör för rät vinkel visa sig. Linjerna är alltså vinkelräta mot varandra.
- Hur kommer det sig att linjen EF blir vinkelrät mot linjen AB? Redovisa ditt resonemang i en text.
- Byt text med en kamrat.
- Har ni tänkt lika? Diskutera med varandra.
- Välj verktyget Visa/Dölj objekt (under verktyget Flytta ritområdet) och sedan först den ena cirkeln och sedan den andra. Välj något annat verktyg, exempelvis Flytta.
- Spara din övning.
Del II - Rita en rät linje som är vinkelrät till en given linje och passerar genom en given punkt
- Öppna ett nytt fönster i GeoGebra och förbered som i förra övningen, genom att dölja axlar, rutnät, Algebra #- # och Inmatningsfönster.
- Välj Inställningar - Namn på objekt - Endast nya punkter
- Rita en linje genom två punkter A och B, med hjälp av linjeverktyget.
- Sätt ut en tredje punkt C någonstans mellan A och B, men inte mitt emellan.
- Rita en cirkel med medelpunkt C, se figur. Du kan zooma ut eller in genom att scrolla.
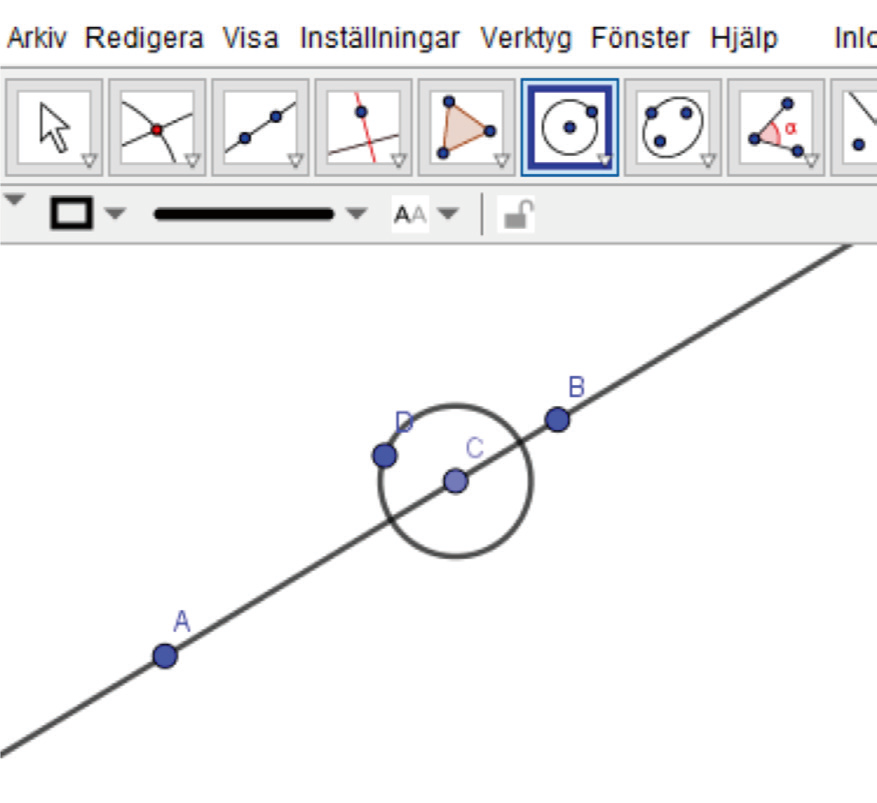
- Använd nu verktygen Cirkel, Skärning mellan två objekt och Linje, för att rita en linje genom C, som är vinkelrät mot AB. Du löser problemet genom att rita ytterligare två cirklar. Fundera på var du ska lägga mittpunkter och skärning med linjen AB.
- Dölj alla cirklar och använd vinkelverktyget för att kontrollera att vinkeln mellan linjerna verkligen är rät.
- Spara ditt arbete.
- Öppna till sist ett nytt fönster. Rita en rät linje och en sträcka och undersök GeoGebras färdiga verktyg Vinkelrät linje, Parallell linje och Mittpunktsnormal.
Del III - Markera mittpunkten på ett linjestycke
- Öppna ett nytt fönster i GeoGebra och förbered genom att dölja axlar, rutnät och så vidare.
- Välj verktyget sträcka och rita ett linjestycke AB.
- Du ska hitta ett sätt att med liknande metod som i tidigare uppgifter markera mittpunkten på AB. Börja med att på rätt sätt konstruera två cirklar.
- När du är klar diskuterar du med en kamrat varför man säkert kan veta att det verkligen är mittpunkten som markerats.
- Spara ditt arbete.
Del IV - Konstruera en liksidig triangel utan att använda verktyget Regelbunden månghörning
- Öppna och förbered ett nytt fönster i GeoGebra, på samma sätt som tidigare.
- Rita en cirkel.
- Rita ytterligare en cirkel. Den andra cirkeln ska ha sin medelpunkt på den första cirkelns rand och sin rand genom den första cirkelns medelpunkt
- Använd Skärning mellan två objekt för att markera cirklarnas skärningspunkter.
- Välj verktyget polygon.
- Klicka på tre lämpliga punkter och sedan tillbaka på den första, så att en liksidig triangel bildas.
- Diskutera med en kamrat hur man säkert kan veta att denna triangel är liksidig.
- Välj verktyget Vinkel.
- Klicka inuti triangeln. Triangelns tre vinklar markeras.
- Kan man av vinklarnas storlek dra slutsatsen att triangeln är liksidig?
- Spara ditt arbete.
Del V - Konstruera parallella linjer
- Öppna och förbered ett nytt fönster i GeoGebra.
- Använd metoder från de tidigare övningarna för att rita två parallella linjer.
|
|
|
#\,#
Svar
Del II - Konstruera en normal genom en given punkt
Markera skärningspunkterna mellan cirkeln och linjen. Konstruera en ny cirkel, med medelpunkt i den ena av dessa skärningspunkter och randen genom den andra. Konstruera ytterligare en cirkel på motsvarande sätt utifrån den andra skärningspunkten. Markera skärningspunkterna mellan de två nya cirklarna. Dra en linje genom dessa skärningspunkter. Se figur.
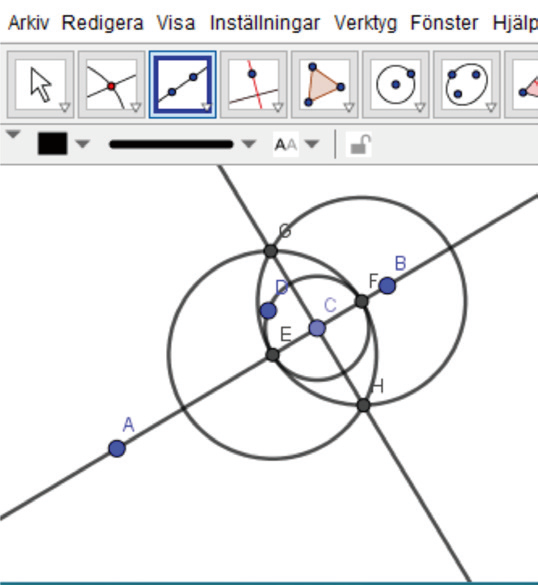
Del III - Markera mittpunkten på ett linjestycke
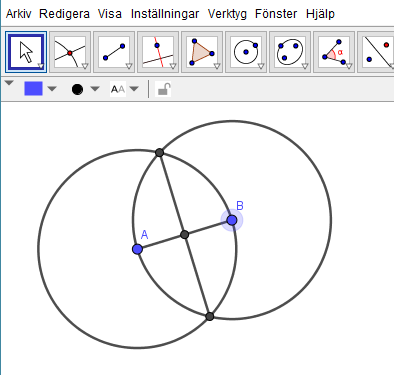
Del V - Konstruera parallella linjer
Konstruera en normal till en normal.
#\,#
 GeoGebra -- Passare och linjal
GeoGebra -- Passare och linjal


















