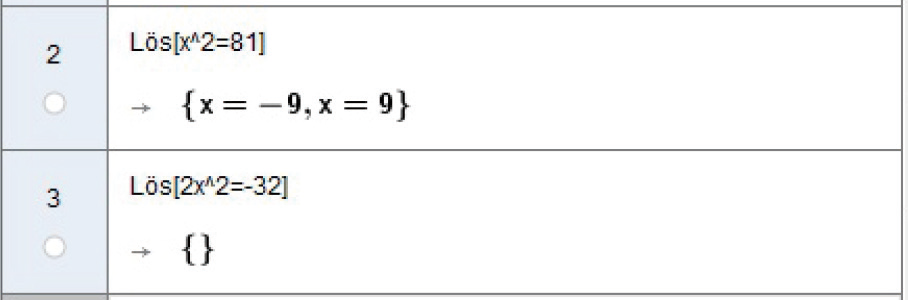GeoGebra Lösa ekvationer

1c 2. Likheter och olikheter: 2.5 Formler och mönster

GeoGebra Lösa ekvationer

Att lösa ekvationer med symbolhanterande verktyg

Med en dator kan du snabbt och enkelt lösa ekvationer. I Geogebra och liknande program finns CAS, Computer Algebra System, som kan användas för algebraisk räkning i matematikuppgifter.

När du har startat Geogebra väljer du CAS från Visa-menyn.

I programfönstret får du ett nytt fönster som har rubriken CAS.

Om du vill lösa ekvationen #5x+7=27 # skriver du Lös #(5 x + 7 = 27) # i CAS-fönstret, följt av returtangenten. Parenteserna är viktiga, innanför dem finns det vi kallar argument. Argumentet för funktionen Lös #() # är alltså i detta fall #5x+7=27 #.

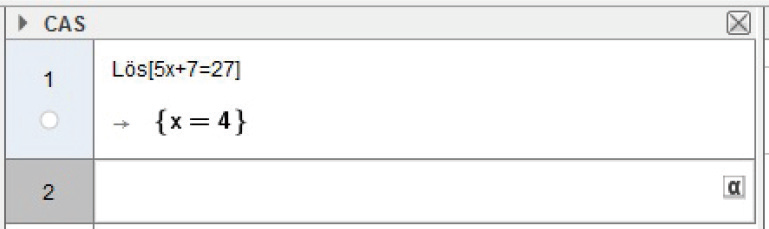
Lösningen är alltså # x = 4. #

Med hjälp av CAS kan du lösa alla typer av ekvationer, till exempel sådana som innehåller potenser. Upphöjt till kan i CAS-fönstret skrivas med tecknet ^. Skriv nu på rad #2 # in Lös#(x^2=81) # och tryck på returtangenten.

Det finns två lösningar, eftersom både #9^{2} = 81 # och #(-9)^{2} = 81. # Ekvationen är ett exempel på en enkel andragradsekvation.

Försök nu med ekvationen #2 x ^{2} = -32. # Du kan skriva antingen #2 x^{2} = -32 # eller #2* x^{2} = -32. # Multiplikationstecknet (*) är inte nödvändigt så länge det är ett tal som multipliceras med variabeln # x . #

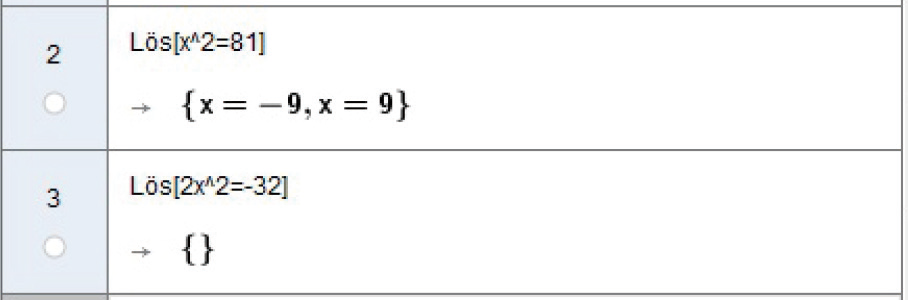
Du får alltså inga lösningar. Varför?

Det finns inga reella tal som löser ekvationen #2 x ^{2} = -32 # och Lös[] letar lösningar endast bland de reella talen.

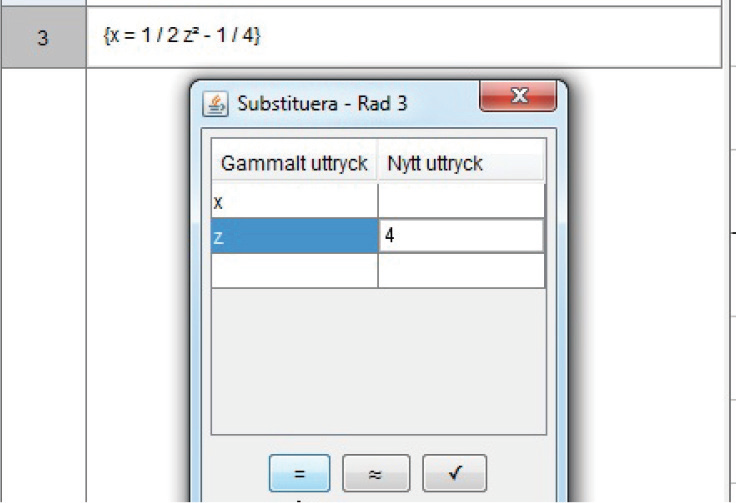
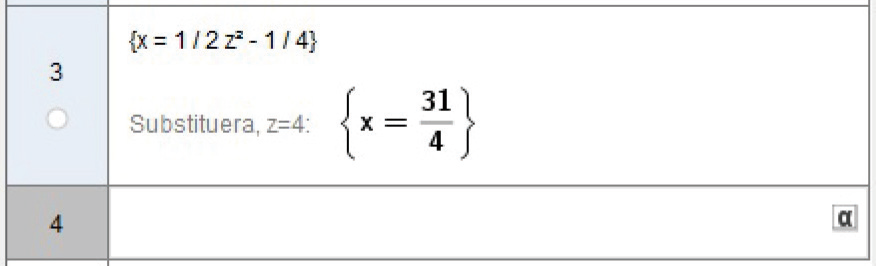
Med CAS kan du också lösa mer invecklade ekvationer, där # x # och andra variabler förekommer på båda sidor om likhetstecknet. Du kan förstås också använda decimaltal i ekvationerna. I Geogebra används punkt (.) som decimaltecken.

Vi löser ekvationen #0,2 x - 4 = 1,4 x + 6 # med CAS.

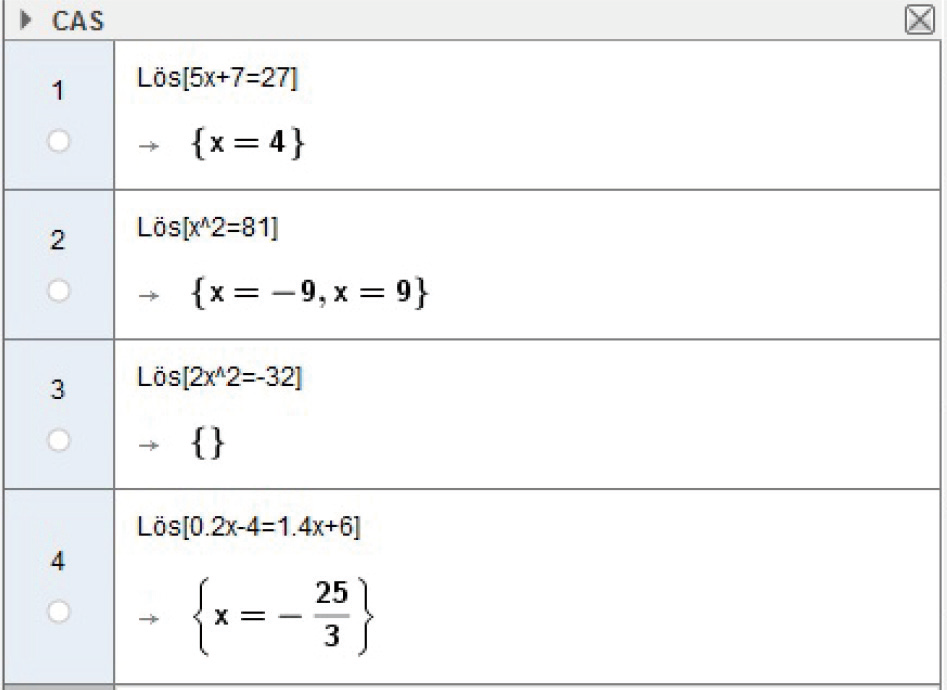
CAS ger svaret i bråkform. Vill du ha ett avrundat värde kan du i menyraden klicka på ikonen

Observera att Geogebra som standard använder två decimaler. Om du vill ha en annan noggrannhet måste du ändra under "Inställningar, Antal decimaler".

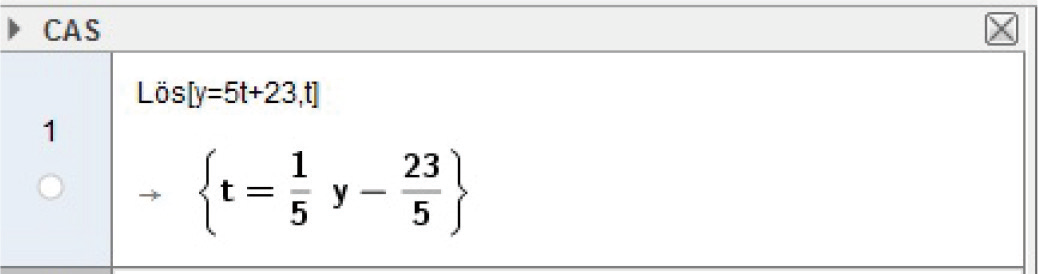
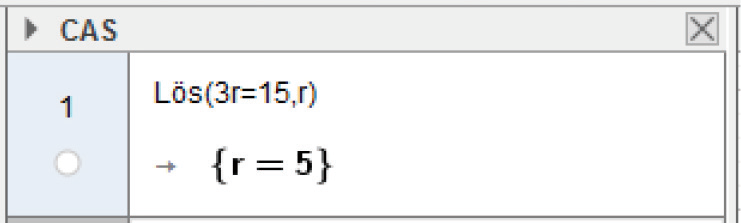
Funktionen Lös() kan lösa ekvationer i andra variabler än #x#, om du kompletterar argumentet med ett komma och sedan den variabel det gäller. För att lösa ekvationen #3 r = 15 # skriver du

UPPGIFTER

Använd CAS för att lösa följande ekvationer.

a) #3x+5=12#

b) #33-5x=32x-300#
a) #1,3 p - 0,9 = 0,8 p #

b) #8,1 n = 3 n + 17 #

c) #0,006 r - 39 = 1,472 r + 5,713 #
Lös om möjligt ekvationerna.

a) # x ^{2} = 8 #

b) # x ^{4} = 39,0625 #

c) #3 x ^{2} + 27 = 0 #

d) # x ^{3}+27= 0 #

e) #(1 + x )^{7} = 78\ 125 #
En cirkel har omkretsen @O = 2pir @, där #r# är cirkelns radie. Hur stor radie har en cirkel med omkretsen

a) #10# meter?

b) @4,27@ cm?

Svara exakt och med två decimalers noggrannhet. För att arbeta med talet @pi@ skriver du "pi" i CAS-fönstret, till exempel 2*pi*r, vilket CAS tolkar som @2pir@.
Arean av en cirkel är # A = \pi r ^{2}#, där # r # är cirkelns radie. Hur stor radie har en cirkel med arean

a) #20# m#^2#?

b) @9,6@ m#^2#?

#\,#

Svar

a) #x=\frac{7}{3}\quad#

b) #x=\frac{333}{37}=9#
a) #p=1,8#

b) #n = \frac{10}{3} \approx 3,33#

c) @r = -30,5@
a) #x=\pm\sqrt{8} = \pm2\sqrt{2}#

b) #x=\pm\frac{5}{2}=\pm2,5#

c) Inga reella lösningar.

d) #x=-3#

e) #x=4#
a) #r=\frac{10}{2\pi}# m # \approx 1,59# m

b) #r=\frac{4,27}{2\pi}# cm # \approx 0,68# cm
a) #r=\sqrt{\frac{20}{\pi}} # m # \approx 2,52# m

b) #r=\sqrt{\frac{9,6}{\pi}} # cm # \approx 1,75# cm

#\,#

#\,#
Att lösa ut variabler och beräkna värden med CAS

Med Lös() kan du också lösa ut en variabel ur en formel. Skriv in formeln och ange efter ett komma vilken variabel som ska lösas ut.

Vi vill lösa ut variabeln # t # ur formeln #y# #=# #5# t #+# #23 # och skriver

CAS kan också hantera mer invecklade uttryck. Om #z=\sqrt {2x + 0,5} # och du ska lösa ut # x # skriver du Lös(z #=# sqrt #(2# x #+0,5)#, x). sqrt är en förkortning av engelskans square root, kvadratrot.

Du kan också bestämma värdet på # x # för ett bestämt värde på #z#. Klicka först på resultatet, där # x # har lösts ut. Uttrycket kopieras då till nästa rad.

I menyraden finns ikonen .

Om du klickar på den visas ett nytt fönster. Där kan du välja vilken av variablerna som ska få ett värde. Om du exempelvis väljer att # z = 4, # skriver du in #4 # som "Nytt uttryck" på raden för z. Därefter klickar du på likhetstecknet, längst ned i samma fönster.

I CAS-fönstret ser du resultatet, uttryckets värde då # z = 4# .

UPPGIFTER

Lös ut variabeln som är angiven inom parentes.

a) # y = 3 x + 5\quad ( x ) #

b) # z = t ^{2} + 4 \quad( t ) #

c) #s = \sqrt {0,6r + 12} \quad(r)#
Lös ut # y # och beräkna värdet på # y # då # x = 9#.

a) #3 x - 2 y = 7 #

b) #2 x - y ^{2} = 12 #
c) #x = {\left( {\frac{{3y}}{4}} \right)^{\tfrac{1}{3}}}#
En modellbil rör sig bort från sin "förare" så att avståndet # s # meter vid tiden # t # sekunder efter start kan beskrivas med formeln # s = 0,6 t + 1,2#. Vid vilken tidpunkt är bilen #10,8 # meter från "föraren"?
För en viss glödlampa kan effekten # P # i watt (W) beräknas med formeln # P = (0,62 I )^{3} # där # I # är strömstyrkan i ampère (A). Hur hög är strömstyrkan då effekten är #11 # W?
Låt #q = \sqrt {\frac{{z - 1}}{{z + 1}}} #.

a) Beräkna värdet på # q # då # z = - 1,01 #

b) Beräkna värdet på # z # då # q = 1,5 #

Uttryck Skriv i CAS-fönstret som

#0,5x#
0.5x

#\sqrt{x+1}# sqrt(x+1)

#4\pi r# 4*pi*r^2

#\left( \frac{4t}{5} \right)^{\frac{1}{3}}# ((4t)/5)^(1/3)

#\,#

Svar

a) #x=\frac{y-5}{3}#

b) #t=\pm\sqrt{z-4}#

c) #r=\frac{5}{3}s^2-20#
a) #y=\frac{3\cdot9-7}{2} = 10#

b) #y=\pm\sqrt{2\cdot 9-12}=\pm\sqrt{6}#

c) #y=\frac{4\cdot 9^3}{3}=972#
#t=16#. Svar #16# s.
#I = \frac{p^{\frac{1}{3}}}{0,62} \approx 3,59#

Svar: #3,59 A#
a) #q=\sqrt{201} \approx 14,18#

b) #z=\frac{-(1,5)^2-1}{1,5^2-1}=-\frac{13}{5}#