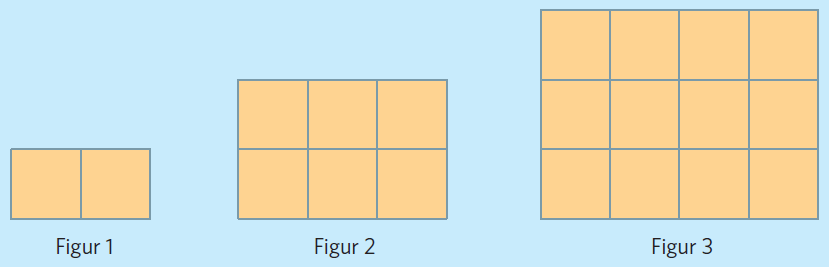
Vi ser att figurerna är rektanglar. Arean på figurerna har samma värde som antalet rutor figuren består av. Vår uppgift är att hitta ett samband mellan antalet rutor, areans storlek, och figurnumret.

Om vi tänker på det sättet ser vi att rektangelns höjd hela tiden är lika stor som figurnumret. Den första figuren har höjden #1, # den andra figuren har höjden #2, # och så vidare.

På samma sätt ser vi att rektangelns bas hela tiden är ett mer än figurnumret: figur #1 # har basen #2, # figur #2 # har basen #3, # och så vidare.

Det innebär att figur # n # har höjden # n # och basen n #+# #1. #

Vi kan nu ställa upp ett uttryck för arean av figur # n # :

#\text{bas} \cdot \text{höjd} = # #( n + 1) \cdot n = n ^{2} + n . #

Antalet rutor i figur # n # kan alltså beskrivas med formeln # a _{ n } = n ^{2} + n #

Vi börjar med att skapa kvadrater eller rektanglar från våra tal, så att vi kan relatera någon av figurens sidor till figurnumret.



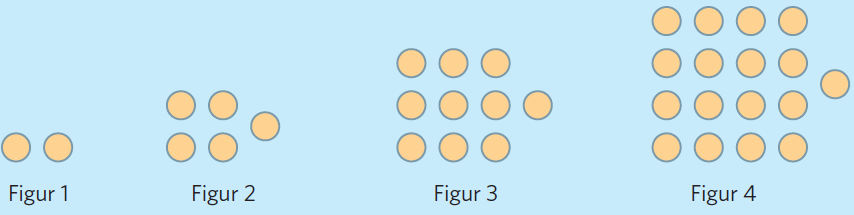
Vi kan se att till exempel tal #3 # är en kvadrat med sidan #3, # plus en extra prick och att tal #4 # är en kvadrat med sidan #4, # plus en extra prick. Man kan tolka även den första figuren som en kvadrat med sidan #1, # plus en extra prick. Alla figurerna är kvadrater, och alla figurerna har en extra prick utanför kvadraten. Kvadraternas sidor är lika långa som figurnumret. Alltså kan talen i vår talföljd beskrivas med formeln # a _{ n } = n ^{2} + 1, # där n är figurnumret.