Om det finns skäl att anta att ett visst statistiskt värde gäller för en hel population och ett stickprov visar ett något annorlunda värde, kan avvikelsen bero på slumpen. Är avvikelsen stor, är det dock troligare att det ursprungliga antagandet om värdet för hela populationen inte stämmer.

Det ursprungliga antagandet om hela populationen kallas för nollhypotesen. Om ett stickprov avviker så mycket från nollhypotesen att man bör dra slutsatsen att nollhypotesen inte stämmer, kallas avvikelsen signifikant.

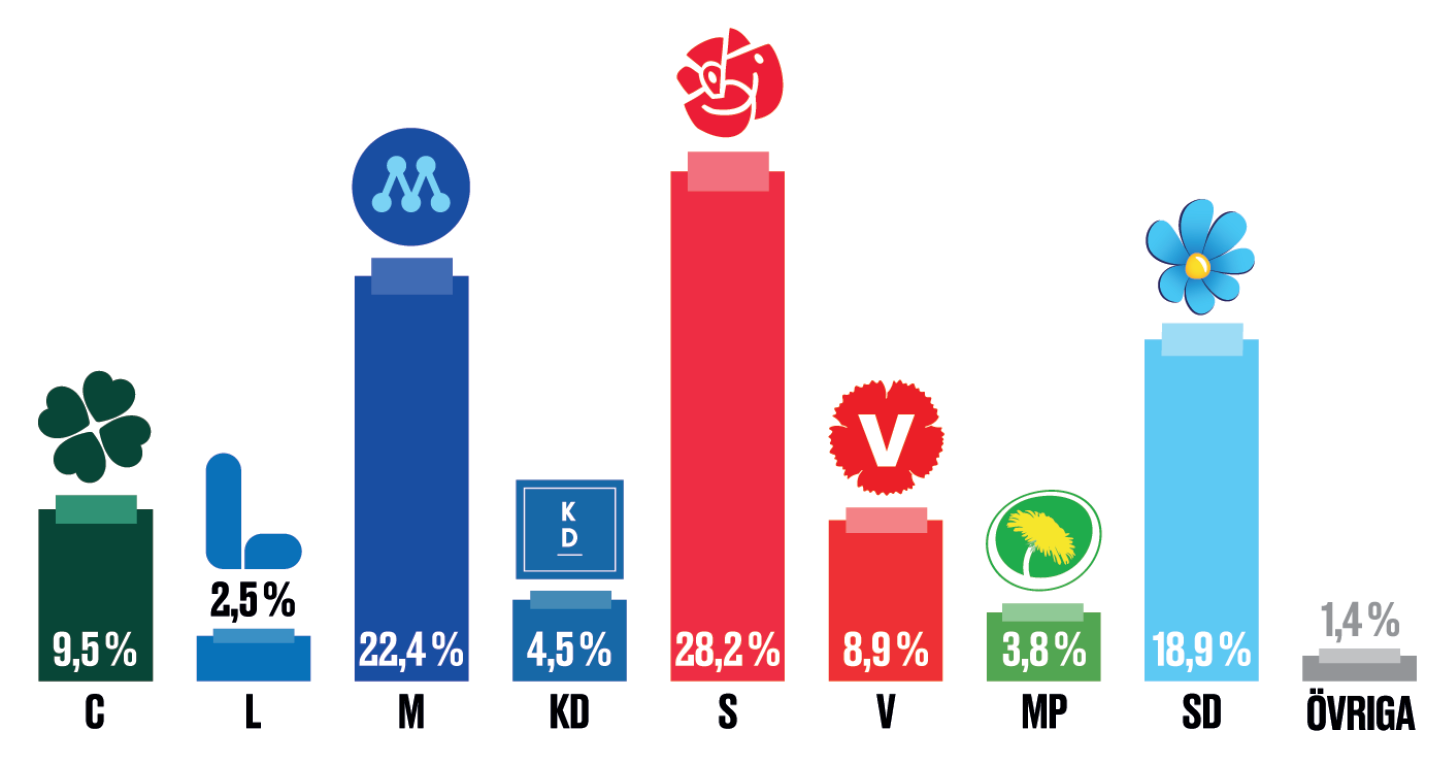
I analysen av väljarundersökningen i den föregående datorövningen utgörs nollhypotesen av partiernas resultat i riksdagsvalet 2018. Stickprovet från den senare väljarundersökningen visar andra värden, men är avvikelserna tillräckligt stora för att man bör dra slutsatsen att stödet för partierna i hela populationen verkligen har förändrats?

I den här typen av väljarundersökningar är det rimligt att arbeta med en gräns på #5~\%#. Hur mycket avviker värdet i stickprovet, det vill säga väljarundersökningen, från nollhypotesen? Och hur stor är sannolikheten för att ett stickprov avviker just så mycket eller mer från nollhypotesen, givet att nollhypotesen är sann? Om denna sannolikhet är större än #5~\%#, antar man att skillnaden mellan nollhypotes och värde för stickprov beror på slumpen. Om sannolikheten är mindre än #5~\%#, antar man att stödet för partiet det gäller verkligen har förändrats, också i hela populationen. Observera alltså att det inte handlar om att avvikelsen i sig skulle var större eller mindre än #5~\%#.

Vi tänker oss att avvikelserna i stickproven fördelar sig symmetriskt över och under det verkliga värdet i polulationen. Om värdet på ett stickprov avviker nedåt från nollhypotesen räknar vi det därför som signifikant, om sannolikheten för ett sådant eller lägre värde är #2,5~\%# eller mindre, givet att nollhypotesen är sann. Motsvarande gäller för värden på stickprov som överstiger nollhypotesen. Värdet på stickprovet räknar vi som signifikant om sannolikheten för ett sådant eller högre värde är #2,5~\%# eller mindre, så länge värdet för hela populationens antas vara enligt nollhypotesen.

I många naturvetenskapliga sammanhang sätter man gränsen för statistisk signifikans mycket lägre än #5~\%#. Inom exempelvis partikelfysik och vid jämförelser av genetiskt material kan det handla om sannolikheter på betydligt mindre än en miljondel. Man vill med andra ord vara mer säker på att en signifikant avvikelse inte beror på slumpen.