1c 5. Statistik: 5.1 Att sammanställa och presentera statistik
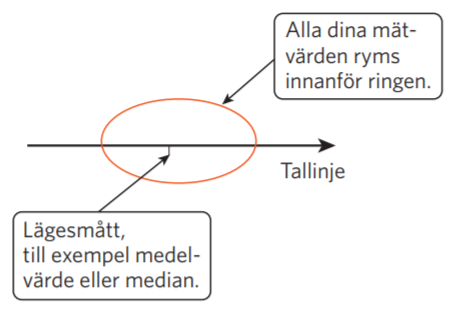
 Lägesmått
Lägesmått
|
Lägesmått Medelvärdet är #\frac{{{\text{summan av alla tal}}\,x}}{{{\text{antalet tal}}\,}}# och betecknas #\bar x#. Medianen är värdet som står i mitten av datamängden när man sorterat alla tal i storleksordning med det minsta talet först. Medianen har lika många tal på sin vänstra sida som på sin högra sida. Om det finns två tal i mitten är medianen medelvärdet av de två mittersta talen. Typvärdet är det vanligaste värdet, det vill säga det värde som förekommer flest gånger. Om det inte går att hitta ett bestämt värde som är vanligast så saknas typvärde. |
Lina har frågat sina klasskamrater om deras skonummer, och sammanfattar resultatet i en tabell. Som exempel kan vi i tabellens andra rad utläsa att #4# personer har skostorlek #36#.
| Skonummer | Frekvens |
| #36# | #4# |
| #37# | #9# |
| #38# | #5# |
| #39# | #3# |
| #40# | #4# |
| #n=25# |
Bestäm lägesmåtten.
På sista raden i tabellen visar Lina att undersökningen omfattar #25 # personer.
Typvärdet är #37, # eftersom flest personer har svarat att de har skonummer #37. #
Medelvärdet är
#\bar x = \frac{{36 \cdot 4 + 37 \cdot 9 + 38 \cdot 5 + 39 \cdot 3 + 40 \cdot 4}}{{25}} = \frac{{944}}{{25}} = 37,76 \approx 38#
Eftersom det är #25 # tal i tabellen är medianen tal nummer #13, # eftersom tal nummer #13 # har #12 # tal före sig och #12 # tal efter sig. Tal nummer #13 # är skonummer #37, # alltså är medianen #37. #
Oskar frågar #10 # av sina kamrater hur många syskon de har, och de svarar så här:
#2, 0, 0, 1, 1, 2, 3, 2, 2, 1 #
Bestäm lägesmåtten.
Medelvärdet är
#(2 + 0 + 0 + 1 + 1 + 2 + 3 + 2 + 2 + 1)/10 = 14/10 = 1,4 # syskon
Typvärdet är #2, # eftersom #2 # förekommer flest gånger.
För att bestämma medianen sorterar Oskar talen i ordning:
#0, 0, 1, 1, 1, 2, 2, 2, 2, 3 #
Eftersom det är ett jämnt antal tal finns det inget enskilt tal som står i mitten, så medianen är medelvärdet av de två mittersta talen. Medianen är #(1 + 2)/2 = 3/2 = 1,5 # syskon.