1c 6. Trigonometri och vektorer: 6.2 Vektorer
 Räta linjen på parameterform
Räta linjen på parameterform
I ett vanligt koordinatsystem är #\vec{e}_x# med koordinaterna #(1,\, 0)# och #\vec{e}_y# med koordinaterna #(0,\,1)# basvektorer. Punkten #P_0# har koordinaterna #(3,\,6)#. Vektorn #\vec{v}# har längden #1# och är ritad som en pil som utgår ifrån #P_0# och är riktad snett uppåt i en vinkel #30°# från den horisontella linjen #y=6#.
Bestäm koordinaterna för #\vec{v}#.
För #30°# gäller de exakta värdena #\sin30° = \frac{1}{2}# och #\cos30°= \frac{\sqrt{3}}{2}#. Vi kan bilda en rätvinklig triangel med en horisontell och en lodrät katet, och där hypotenusan utgörs av #\vec{v}#. Hypotenusan har längden #1#, den horisontella katetn längden #\frac{\sqrt{3}}{2}# och den lodräta kateten längden #\frac{1}{2}#.
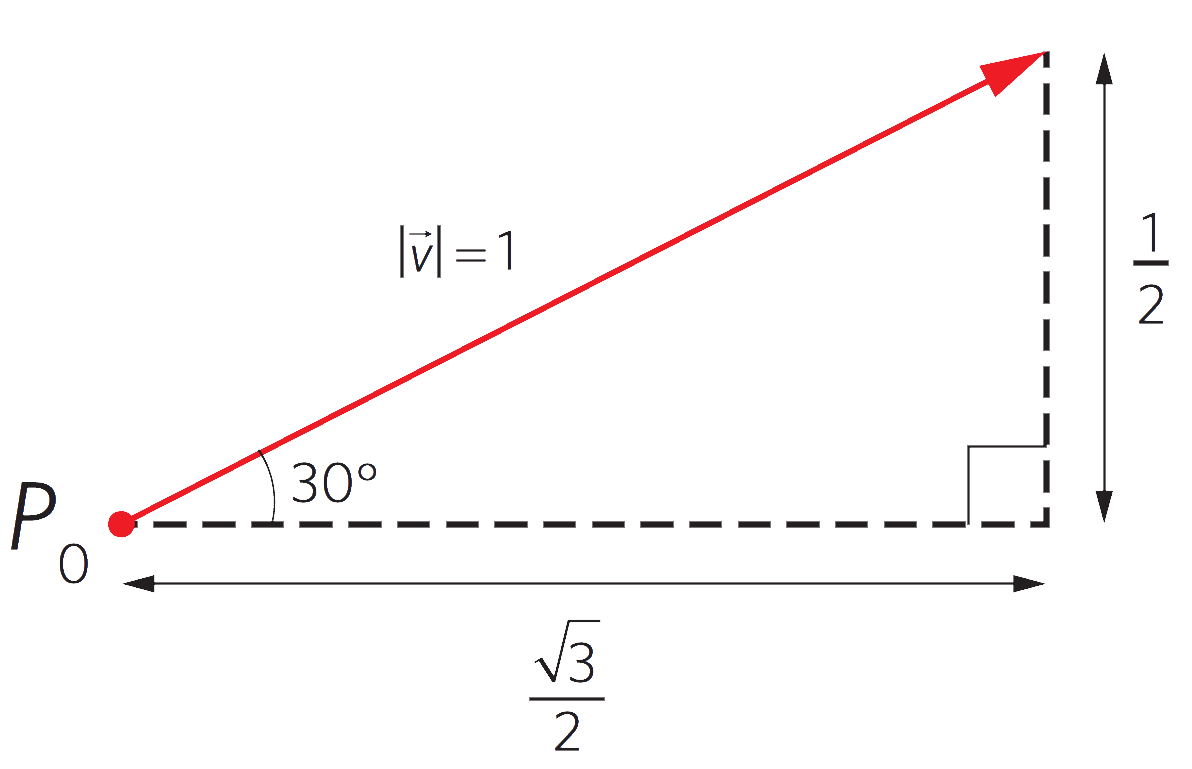
Svar: Koordinaterna för #\vec{v}# är #\bigg( \frac{\sqrt{3}}{2},\, \frac{1}{2}\bigg)#.
Låt koordinatsystemet i det föregående exemplet visa ett hav, där #x#-axeln är riktad mot öst och #y#-axeln mot norr. Basvektorerna #\vec{e}_x# och #\vec{e}_y# har båda längden #1# sjömil.
Låt #t# vara tiden i timmar. Vi tiden #t=0# passerar ett fartyg punkten #P_0#. Fartygets fart är #15# knop, det vill säga #15# sjömil per timme, det håller rak kurs och dess hastighet är #15\vec{v}#.
Vilken kommer fartygets position i koordinatsystemet att vara vid #t=2# och vad var den vid #t=-1#?
För positionen vid #t=2# gäller för #x#-koordinaten #3+2 \cdot 15 \cdot \frac{\sqrt{3}}{2} \approx 29,0# och för #y#-koordinaten #6+2 \cdot 15 \cdot \frac{1}{2}=17#. Vid #t=-1# gäller för #x#-koordinaten #3-1 \cdot 15 \cdot \frac{\sqrt{3}}{2} \approx -10,0# och för #y#-koordinaten #6-1 \cdot 15 \cdot \frac{1}{2} = -1,5#.
Svar: Vid #t=-1# var fartygets position i koordinatsystemet #(-10,\,-1,5)#, vid #t=2# kommer den att vara #(29,\, 17)#.
Alla punkter som ges när #15t# varierar i #(3,\,6)+15t\vec{v}# ligger på en rät linje, som går genom #P_0# och är parallell med #\vec{v}#. När #t# varierar i #(3,\,6)+t\vec{v}# får vi förstås punkter på samma räta linje. Ställer vi upp en ekvation för linjens #x#-koordinater och en för dess #y#-koordinater får vi systemet
#\left\{ \begin{array}{l} x=3+ \displaystyle\frac{\sqrt{3}t}{2}\\ y=6+ \displaystyle\frac{t}{2} \end{array} \right.#
Här kallas #t# för parameter. Att visa en rät linje med denna typ av system kallas för att sätta en rät linje på parameterform. #t# varierar, men har samma värde i båda ekvationerna.
Räta linjen på parameterform
En rät linje som går genom punkten med koordinater #(x_0,\,y_0)# och har lutningen #\frac{\beta}{\alpha}#, kan uttryckas med #t# som parameter enligt #\left\{ \begin{array}{l} x=x_0+\alpha t \\ y=y_0+\beta t \end{array} \right.#.


