Trigonometri

1c 6. Trigonometri och vektorer: 6.1 Trigonometri

Trigonometri

Trigonometri är den del inom matematiken som behandlar samband mellan vinklar och sidor i en triangel. Trigonometri används för att bestämma positioner och avstånd inom områden som astronomi, lantmäteri och arkitektur. Med hjälp av trigonometri kan vi till exempel bestämma avståndet mellan två stjärnor, eller steghöjden i en trappa. Trigonometriska samband går att tillämpa på alla trianglar, men vi begränsar oss här till rätvinkliga trianglar.

Ordet trigonometri är sammansatt av det grekiska trigonon, som betyder "tre vinklar", och metron, som betyder "mått".

Vi inför tre nya begrepp i en rätvinklig triangel: närliggande katet till vinkeln $v ,$ motstående katet till vinkeln $v$ och hypotenusa.

$\,$

Kontroll

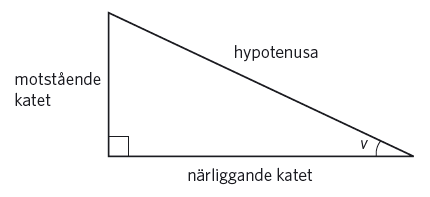
a) Hur lång är motstående katet till vinkel $v$ ?

b) Hur lång är närliggande katet till vinkeln $v$ ?

c) Hur lång är motstående katet till vinkel $u$ ?

d) Hur lång är närliggande katet till vinkeln $u$ ?

Svar

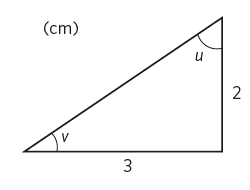a) $2$ cm

b) $3$ cm

c) $3$ cm

d) $2$ cm

$\,$

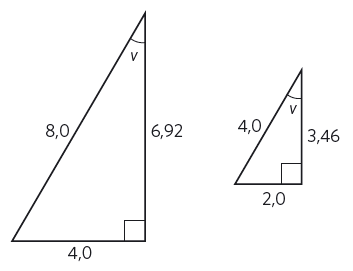
Vi studerar två likformiga trianglar.

Båda trianglarna har en rät vinkel och en vinkel $v$ .

Vi tecknar tre olika kvoter för de två trianglarna:

$\frac{{{\text{motstående katet}}}}{{{\text{hypotenusan}}}} = \frac{{4,0}}{{8,0}} = \frac{{2,0}}{{4,0}} = 0,5$

$\frac{{{\text{närliggande katet}}}}{{{\text{hypotenusan}}}} \approx \frac{{6,92}}{{8,0}} = \frac{{3,46}}{{4,0}} \approx 0,865$

$\frac{{{\text{motstående katet}}}}{{{\text{närliggande katet}}}} \approx \frac{{4,0}}{{6,92}} = \frac{{2,0}}{{3,46}} \approx 0,578$

Kvoterna beror av vinkelns storlek. De har samma värde för alla rätvinkliga, likformiga trianglar oberoende av triangelns storlek.

Dessa kvoter används ofta och har därför fått särskilda namn. De kallas sinus för $v ,$ cosinus för $v$ och tangens för $v$ och förkortas sin $v ,$ cos $v$ och tan $v$ .

Definition sinus, cosinus och tangens för vinkeln v

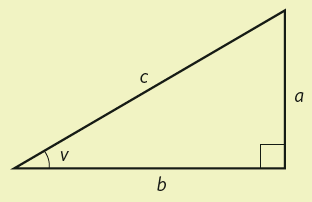
${\text{sin }}v = \frac{{{\text{motstående katet}}}}{{{\text{hypotenusan}}}} = \frac{a}{c}$

${\text{cos }}v = \frac{{{\text{närliggande katet}}}}{{{\text{hypotenusan}}}} = \frac{b}{c}$

${\text{tan }}v{\text{ }} = {\text{ }}\frac{{{\text{motstående katet}}}}{{{\text{närliggande katet}}}} = \frac{a}{b}$

Kvoterna beror av vinkeln och utgör ett mått på vinkelns storlek.

Bestäm $sin (v)$ , $cos (v)$ och $tan(v)$ .

$\sin v = \frac{3}{{\sqrt {45} }} \approx 0,45$

$\cos v = \frac{6}{{\sqrt {45} }} \approx 0,89$

$\tan v = \frac{3}{6} = 0,50$

Nästa exempel

Bestäm sidan $a$ .

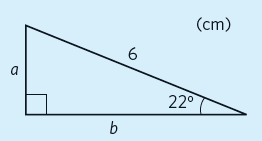
Vi använder räknarens tangenter för $sin(v)$ , $cos(v)$ och $tan(v)$ när vi känner en vinkel.

$\sin (22°) = \frac{a}{6}$

$a = 6 \cdot \sin(22°) ≈ 2,25$

Vinkeln $22°$ och hypotenusan är givna och vi ska bestämma motstående katet. Därför väljer vi sinus.

Den motstående kateten är ungefär $2,25$ cm.

Nästa exempel

1c 6. Trigonometri och vektorer: 6.1 Trigonometri

Trigonometri

Hur kan AI-boten hjälpa dig?