1c 6. Trigonometri och vektorer: 6.2 Vektorer
 Vektorer
Vektorer
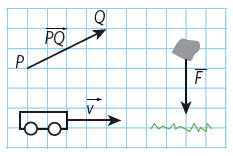
Med en storhet menar vi en egenskap som går att mäta och beräkna. Några exempel på storheter är vikt, längd, tid och kraft. Vissa storheter, till exempel kraft, har både storlek och riktning. De kallas vektorer eller vektorstorheter. Andra storheter, till exempel vikt, har enbart storlek. De kallas skalärer eller skalära storheter.
Om # k = 0 # får vi en vektor som är #0 # längdenheter lång. Den vektorn kallas nollvektorn, och saknar riktning. Nollvektorn betecknas #\vec 0#.
|
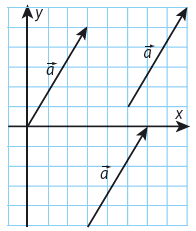
Vektorer En storhet är något som kan mätas och beräknas. En skalär storhet har bara en storlek. En vektorstorhet har både storlek och riktning. En vektor från punkten #P# till punkten #Q# betecknas #\vec {PQ}#, och dess längd betecknas #|\vec {PQ}|#. En vektor #\vec a# kan multipliceras med ett tal #k#. Resultatet är en vektor med samma riktning och som är #k# gånger längre, om #k > 0#. Vektorerna #\vec a# och #-\vec {a}# är motsatta vektorer. De är lika långa men har motsatt riktning. |
Vektorn #\vec a# är #6 # längdenheter lång.
Vad händer om vi multiplicerar vektorn med @k=1,5@ och #k= -2#?
Vi multiplicerar den med talet # k = 1,5 # och får en vektor med samma riktning, och som är #9 # längdenheter lång.
Vi multiplicerar #\vec a# med talet # k = -2 # och får en vektor som har motsatt riktning, och som är #12 # längdenheter.
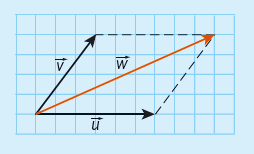
Vi kan addera två vektorer #\vec u# och #\vec v# och får då en ny vektor, #\vec u + \vec v = \vec w#. Summan av två eller flera vektorer kallas ofta resultanten till de adderade vektorerna.
- Vi skapar en parallellogram utifrån de vektorer #\vec u# och #\vec v# som ska adderas. Det gör vi genom att placera vektorerna så att de har gemensam startpunkt, och därefter drar vi streckade linjer så att vi får en parallellogram. Resultanten #\vec w# är en vektor från den gemensamma startpunkten till motstående hörn i parallellogrammen. Detta kallas parallellogrammetoden.
- Vi kan också placera vektorerna efter varandra, så att den första vektorns slutpunkt är den andra vektorns startpunkt. Den metoden kallas polygonmetoden. Summan av vektorerna är en vektor från den första vektorns startpunkt till den sista vektorns slutpunkt.
Vi kan också subtrahera vektorer. Med differensen #\vec u - \vec v# menar vi resultanten till vektorerna #\vec u# och # - \vec v#, eftersom vi vill att #\vec u - \vec v = \vec u + (-\vec v)#.
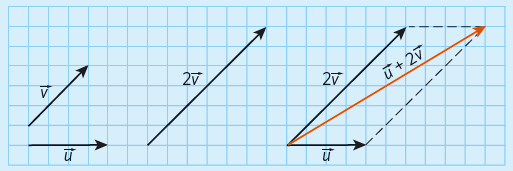
Börja med att rita vektorn #2\vec v#. Använd sedan antingen parallellogram- eller polygonmetoden för att rita summan.