Vektorer i koordinatform

1c 6. Trigonometri och vektorer: 6.2 Vektorer

Vektorer i koordinatform

Vektorn #\small{\vec {PQ}} # börjar i punkten #(1, 2) # och slutar i punkten #(5, 3)#. För att gå från # P # till # Q # behöver vi förflytta oss #4 # steg i # x #-riktningen och #1 # steg i # y #-riktningen. Vi säger att koordinaterna för vektorn #\small{\vec {PQ}} # är #(4, 1). # En vektors koordinater beskriver hur vi ska förflytta oss från startpunkten # P # till ändpunkten # Q # i ett rätvinkligt koordinatsystem.

Vektorn #\small{\vec {OP}} # kallas ortsvektor då den utgår från origo. Den kan beskrivas med hjälp av koordinaterna för punkten # P , # eftersom origo har koordinaterna #(0, 0)#. #\small{\vec {OP}}# #= (1,\,\,2)#.

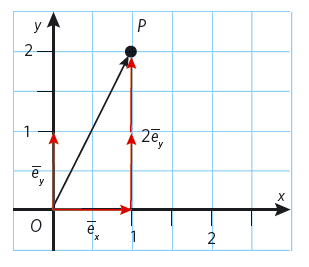
Ett annat sätt att beskriva vektorer är genom att införa basvektorer eller enhetsvektorer. I ett standard-koordinatsystem är en basvektor en vektor med längden #1 # längdenhet och som är parallell med en koordinataxel i dess positiva riktning. I ett tvådimensionellt koordinatsystem har vi basvektorerna #{\vec e_x}# som har koordinaterna #(1, 0) # och #{\vec e_y}# som har koordinaterna #(0, 1). # För att skapa en vektor med hjälp av basvektorerna undersöker vi hur många basvektorer vi behöver lägga efter varandra för att nå från startpunkt till slutpunkt.

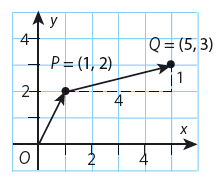
Vektorn #\overrightarrow {OP} # kan beskrivas med vektorsumman #1 \cdot {\vec e_x} + 2 \cdot {\vec e_y} = (1,\,\,2)#. Talen #1 # och #2 # är vektorns koordinater med avseende på basvektorerna #{\vec e_x}# och #{\vec e_y}#. Vektorerna #1 \cdot {\vec e_x}# och #2 \cdot {\vec e_y}# kallas vektorns komposanter.
I ett standardkoordinatsystem talar man ofta om # x#- och # y #-komposanter, och dessa bildar alltid rät vinkel med varandra.

På samma sätt kan vektorn #\vec {PQ} # i övre figuren beskrivas med #4 \cdot {\vec e_x} + 1 \cdot {\vec e_y} = (4,\,\,1)#. Från punkten # P # behöver vi #4 # basvektorer i # x #-riktningen och #1 # basvektor i # y #-riktningen för att nå punkten # Q . # Med två exempel visar vi nu hur man räknar med vektorer i koordinatform.

Vi har punkterna # P = (2, 3) # och # Q = (7, 2). # Skriv vektorn #\vec {PQ} # som en addition av basvektorer och i koordinatform.

#\vec {PQ} = 5 \cdot {\vec e_x} + ( - 1) \cdot {\vec e_y} = (5,\,\, - 1)# eftersom vi går #5 # steg i # x #-riktningen och #(-1) # steg i # y #-riktningen.

Nästa exempel

Vektorn #\vec u = (2,\;4)# och vektorn #\vec v = (3,\; - 1)#. Bestäm summan #\vec u + \vec v#.

Vi kan direkt addera koordinaterna:

#(2, 4) + (3, -1) = (2 + 3, 4 - 1) = (5, 3) #

Nästa exempel

På samma sätt kan vi visa hur subtraktion av vektorer fungerar, och även multiplikation av en vektor med ett tal. Det ger oss tre räkneregler för vektorer i koordinatform.

Räkneregler för vektorer i koordinatform

#( x _{1}, y _{1}) + ( x _{2}, y _{2}) = ( x _{1} + x _{2}, y _{1} + y _{2}) #

#( x _{1}, y _{1}) - ( x _{2}, y _{2}) = ( x _{1} - x _{2}, y _{1} - y _{2}) #

# k \cdot ( x , y ) = ( kx , ky ) #

Längden av en vektor i ett rätvinkligt koordinatsystem kan vi beräkna med hjälp av Pythagoras sats. Om vektorn #\vec v = (x,\;y)# så är längden #\left| {\vec v} \right| = \sqrt {{x^2} + {y^2}} #

En vektors längd kan också kallas dess storlek, belopp eller absolutbelopp.

Vad är längden av vektorn #\vec v = (5,\;3)#?

#\left| {\vec v} \right| = \sqrt {{5^2} + {3^2}} = \sqrt {25 + 9} = \sqrt {34} # längdenheter.

Nästa exempel

Beräkna #|\vec u + 2\vec v|# om #\vec u = (-2, 3)# och #\vec v = (3, -1)#

Vi beräknar #\vec u + 2\vec v# #= (-2, 3) + 2 \cdot (3, -1) = (-2, 3) + (6, -2) = (-2 + 6, 3 - 2) = (4, 1) #

#\left| {\vec u + 2\vec v} \right| = \sqrt {{4^2} + {1^2}} = \sqrt {16 + 1} = \sqrt {17} #

Nästa exempel