Diskutera, resonera och modellera

1c 6. Trigonometri och vektorer: 6.2 Vektorer

Diskutera, resonera och modellera

Kraft och acceleration Nivå 1

I fysiken arbetar man med vektorer för att beräkna den resulterande kraften på ett föremål.

Fall med luftmotstånd

Ett föremål som faller utan luftmotstånd påverkas bara av en kraft, den nedåtriktade tyngdkraften. Storleken på kraften är #F = mg#, där #m# är föremålets massa och #g# är gravitationsaccelerationen. I Sverige är gravitationsaccelerationen #9,82# m/s#^2#, riktad mot jordens centrum.

Skriv gravitationsaccelerationen som en vektor i koordinatform.
Beräkna tyngdkraften på ett föremål som har massan #m = 50# kg. Svara med en vektor i koordinatform.
Luftmotståndet är en uppåtriktad kraft. Vi antar att luftmotståndet har storleken #F = kv^2#, där #k# är en konstant och #v# är föremålets hastighet nedåt. Skriv luftmotståndskraften som en vektor.
Ett föremål med massan #m# faller med hastigheten #v#. Bestäm den resulterande kraften på föremålet, det vill säga vektorsumman av tyngdkraften och luftmotståndskraften.
Om den resulterande kraften #\vec R = \vec 0# kommer det fallande föremålet att röra sig med konstant hastighet. Bestäm ett uttryck för den konstanta hastigheten för ett föremål med massan #50# kg som faller med luftmotstånd.
Beräkna hur fort en fallskärmshoppare som väger #65# kg faller, om #k = 197# kg/m.
#\,#

#\,#

Svar

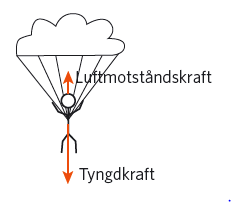
Gravitationsaccelerationen #\vec{g} = (0; - 9,82)# m/s#^2#
Om #m = 50# kg är tyngdkraften @\vec{F} = 50\vec{g} = (0; -9,82 * 50)@#\rm{N}# @= (0, -491)@#\rm{N}#
Luftmotståndskraften @\vec{F_L} = (0; kv^2)@
Resultanten av tyngdkraften och luftmotståndskraften är @\vec{R} = (0; -491)@#\rm{N} + (0; kv^2) = (0; kv^2-491 \rm{N})#
Resultanten är #0# om @kv^2 - 491@#\rm{N} = 0#, så @v = sqrt(491/k)@ m/s.
Om #m = 65# kg och #k = 197# kg/m är @\vec{R} = (0; -9,82 * 65)@#{\rm N} + (0; 197 \text{ kg/m } \cdot v^2) = (0; 197 \text{ kg/m } \cdot v^2 - 638{,}3 {\rm N})#
Resultanten är #0# om #197 \text{ kg/m } \cdot v^2 - 638,3 {\rm N} = 0#, så @v = sqrt(638,3/197)@ m/s @ \approx 1,8@ m/s.

#\,#

Kraft och acceleration Nivå 2

Krafter på en boll som rullar nedför en backe

Om det finns en resulterande kraft på ett föremål kommer föremålet att accelerera, det vill säga öka farten i kraftens riktning. Vi vet av erfarenhet att en boll som rullar utför en backe ökar sin fart, det vill säga accelererar. Det som ger upphov till accelerationen är en komposant av tyngdkraften #\vec F_g#, i figuren kallad #\vec F_x#, som är en kraft i backens riktning.

En boll med massan #m = 5,0# kg rullar utför en backe. Backen är #50# meter lång och höjdskillnaden är #4# meter. Se figur.

Bestäm vinkeln #v#. Svara med en decimals noggranhet.
Bestäm tyngdkraften på bollen. Använd #g = 9,82# m/s#^2#.
De två trianglarna i figuren, det vill säga backen och den triangel som bildas av kraftvektorerna, är likformiga. Hur kan man se det?
Bestäm storleken på komposanterna #F_x# och #F_y# med hjälp av likformighet.
Bestäm storleken på komposanterna med hjälp av trigonometri.
Hur stor är bollens acceleration utför backen? Enligt Newtons andra lag är #\vec F = m\vec a#, och storleken på kraften är #|\vec F| = m \cdot |\vec a| = m \cdot a#.
Om bollen släpps från backens topp gäller följande samband mellan sträcka, acceleration och tid: @s = (at^2)/2@. Hur lång tid tar det för bollen att rulla utför hela backen?
Skapa ett eget, liknande problem, där du själv bestämmer bollens massa och backens lutning. Ta reda på hur lång tid det tar för bollen att rulla utför backen. Du kan förstås följa beräkningsstegen här ovanför.

#\,#

Svar

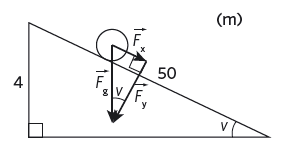
@sin(v) = 4/50@, så @v = 4,6°@.
@\vec{F_g} = (0; -9,82 * 5)@#{\rm N} = #@(0; -49,1)@#{\rm N}#
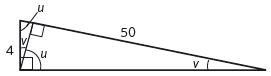
Om vi ritar en sträcka från backens rätvinkliga hörn i rät vinkel upp mot den sluttande sidan, får vi två nya, mindre trianglar.

I figuren gäller @u + v = 90°@. Eftersom vinkeln #u# är gemensam för den störstsa triangeln och den minsta triangeln, måste den minsta triangelns andra vinkel vara #v#. Det innebär att trianglarna är likformiga, eftersom vinklarna är lika stora.
Likformighet ger @(|\vec{F_g}|)/50 = 49,1/50 = (|\vec{F_x}|)/4@, alltså är @|\vec{F_x}| = (4*49,1)/50 \approx 3,9@ dvs. @\vec{F} \approx 3,9@#\rm{N}#

Med pythagoras sats får vi då @3,9^2 + |\vec{F_y}|^2 = 49,1^2@, vilket ger @|\vec{F_y}| = sqrt(49,1^2 - 3,9^2)@, dvs. @\vec{F_y} \approx 48,9@

Använder vi trigonometri får vi @|\vec{F_x}| = |\vec{F_g}|sin(v) = 49,1sin(4,6°) \approx 3,9@ och @|\vec{F_y}| = |\vec{F_g}|cos(v) = 49,1cos(4,6°) \approx 48,9@

Utför backen verkar kraften #3{,}9 \rm{N}#. Accelerationen @a = 3,9/5@ m/s#^2 = 0,78# m/s#^2#.

@s = (at^2)/2@ ger @t = sqrt((2s)/a) = sqrt((2*50)/0,78) \approx 11,3@

Svar: @11,3@ s

#\,#