Vektorer i GeoGebra

Det finns två sätt att skapa vektorer i GeoGebra. Du kan dels använda Inmatningsfältet och dels använda verktyget Vektor, som ligger under verktyget Linje i verktygsfältet.

När du har markerat vektorverktyget klickar du på två ställen i Ritområdet för att rita din vektor.

Om du vill skapa en vektor genom att använda Inmatningsfältet kan du arbeta på två sätt. Du kan skriva v = vektor((3,1)) i Inmatningsfältet (notera de dubbla parenteserna), och trycka på returtangenten. Då skapas en vektor #v# som utgår från origo och har spetsen i #(3, 1)#. Du kan också skriva u = vektor((2,1), (3,5)). Då skapas en vektor som utgår från #(2, 1)# och har spetsen i #(3, 5)#.

Det är förstås också möjligt att addera och subtrahera vektorer. Öppna ett nytt fönster. Mata in vektorerna v = vektor((3,1)) och u = vektor((-2,3)). Därefter skriver du w = v + u i Inmatningsfältet, och trycker på returtangenten. I Ritområdet ser du vektorn # w # som är summan av vektorerna #v# och #u#, och i algebrafönstret till vänster ser du att w = (1, 4). För vektorer visas koordinaterna uppställda vertikalt.

UPPGIFTER

1. Använd GeoGebra för att beräkna #\vec{u} + \vec{v}# om

   a) #\vec{u} = (1, 5)# och #\vec{v} = (2, -5)#

   b) #\vec{u} = (-2, 3)# och #\vec{v} = (2, 1)#

   c) #\vec{u} = (3, 3)# och #\vec{v} = (-2, -2)#

2. Använd GeoGebra för att beräkna #\vec{u} - \vec{v}# om

   a) #\vec{u} = (2, 2)# och #\vec{v} = (1, -1)#

   b) #\vec{u} = (3, 6)# och #\vec{v} = (-2, 5)#

   c) #\vec{u} = (-1, 3)# och #\vec{v} = (-2, -4)#

3. Skapa en glidare #s# och en vektor #\vec{u}# genom att skriva u = s*vektor((2,0)) i inmatningsfältet, följt av returtangenten.

   Bekräfta "Ja, skapa ny glidare".

   Klicka och dra glidarens punkt och studera hur vektorn förändras.

   Hur lång är vektorn då #s = 2,4#? Varför?

Vektorlängd

Med GeoGebra och CAS kan du beräkna längden av en vektor.

Skriv in u = vektor((3,5)) i Inmatningsfältet följt av returtangenten.

Öppna CAS-fönstret genom att från Visa-menyn välja CAS.

Klicka i CAS-fönstret, och skriv Längd(u) följt av returtangenten. CAS svarar @sqrt(34)@. Pythagoras sats ger ju att vektorns längd är exakt @sqrt(3^2+5^2) = sqrt(34)@. Skriver du i stället Längd(u) i Inmatningsfältet och trycker retur får du ett närmevärde.

Komposanter och trigonometri

Börja med att skapa två glidare i ett nytt fönster i GeoGebra.

Använd verktyget

Välj Glidare och klicka någonstans i Ritområdet. Ändra den första glidarens Namn till #r#, sätt "Min:" till #0# och låt "Max:" fortsatt vara #5#. Den andra glidaren kallar du #v#, och den ska kunna varieras mellan #0# och #90#.

Skapa en vektor # u # med hjälp av kommandot u = vektor (( r;v°)). Observera semikolon mellan #r# och #v#, och ring för grader efter #v#. Gradtecknet #°# hittar du genom att klicka på alfa-symbolen #α# till höger om Inmatningsfältet.

Vektorn # u # utgår nu från origo och har längden # r#. Vektorn bildar vinkeln # v °# med den positiva # x #-axeln.

Välj Inställningar, Antal decimaler och ändra till #5 # decimaler.

Dra glidaren #r# till r #= 5#. Vektorn # u # får då längden #5 # längdenheter.

Dra sedan glidaren v till v #= 45#. Vad händer med koordinaterna för vektorn # u # ?

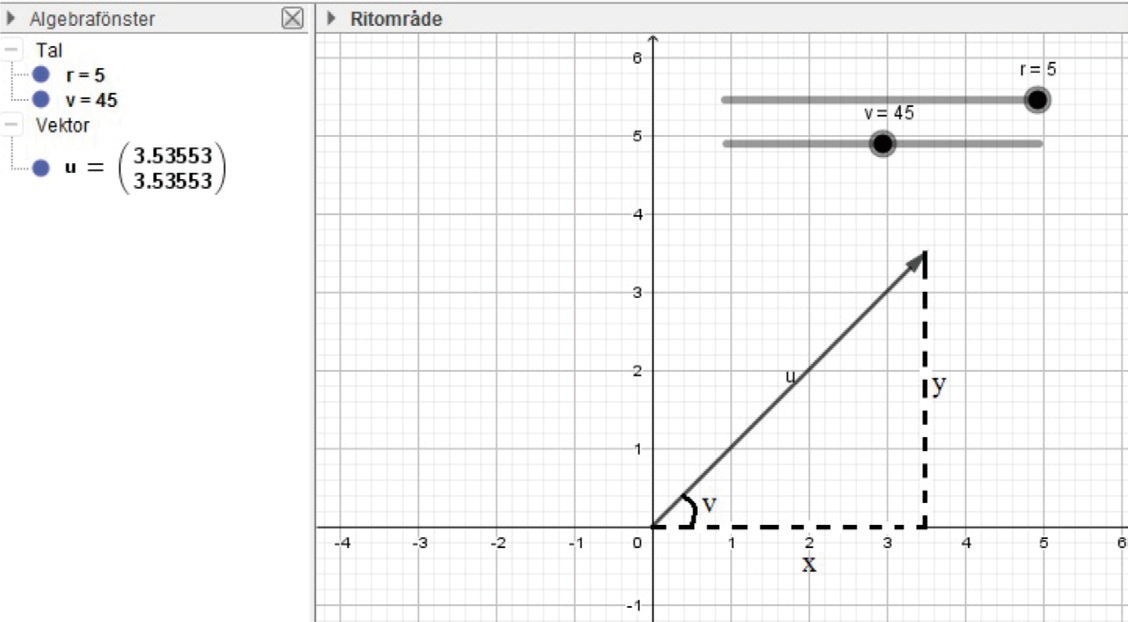
Vektorn # u # bildar vinkeln # v = 45°# med # x #-axeln i koordinatsystemet. I bilden ovan har vi markerat vinkeln. Vi har också skapat en rätvinklig triangel genom att rita en sträcka från vektorn # u #:s spets ner till # x #-axeln, och där­ifrån en annan sträcka vidare till origo.

Hur långa är sträckorna # x # och # y # i figuren? Med hjälp av trigonometri kan vi beräkna deras längder:

#\cos 45° = \frac{x}{5}# ⇒ # x = 5 \cos 45°# ≈ @3,53553@

#\sin 45° = \frac{y}{5}# ⇒ # y = 5 \sin 45°# ≈ @3,53553@

Värdena är alltså desamma som vektorn # u #:s # x#- och # y #-koordinater, som du kan läsa av i Algebrafönstret.

Sträckorna # x # och # y # kan beskrivas med hjälp av vektorerna

#\vec x = (3,53553;\,0)# och #\vec y = (0;\,3,53553)#.

Summan av vektorerna är

#\vec x + \vec y = (3,53553;\,0) + (0;\,3,53553)\, = (3,53553;\,3,53553) = \vec u#

Vi kallar vektorerna # x # och # y # för komposanterna till vektorn # u #. Komposanter till en vektor # u # är två vinkelräta vektorer vars summa är # u #. Att kunna beräkna komposanter är viktigt framför allt i fysiken, när du arbetar med krafter.

#\,#

UPPGIFTER

1. Bestäm genom att läsa av i Algebrafönstret #x#- och #y#-komposanterna till vektorn #u# då

   a) #r = 4# och #v = 60°#

   b) #r = 3# och #v = 70°#

   c) #r = 5# och #v = 30°#

   d) #r = 1# och #v = 37°#

   Tips: Det kan vara svårt att få exakta värden genom att dra i glidarna. Klicka då istället på talen #r# och #v# i Algebrafönstret och skriv in värdena direkt.

2. Modifiera glidaren #v# så att den kan varieras mellan #0°# och #180°#. Bestäm #x#- och #y#-komposanterna till vektorn #u# då

   a) #r = 4# och #u = 120°#

   b) #r = 3# och #v = 110°#

   c) #r = 5# och #v = 150°#

   d) #r = 1# och #v = 143°#

   Jämför dina svar på uppgifterna #1# och #2#. Kan du förklara likheterna och skillnaderna?

3. Hur ska du gå till väga för att bestämma @cos(23°)@ och @sin(23°)@ endast med hjälp av vektorn #u# och glidarna #r# och #v#.

4. Bestäm med metoden i uppgift #3# med #5# decimalers noggrannhet

   a) @cos(82°)@ och @sin(82°)@

   b) @cos(60°)@ och @sin(60°)@

   c) @cos(135°)@ och @sin(135°)@

   c) @cos(180°)@ och @sin(180°)@