1c 6. Trigonometri och vektorer: 6.1 Trigonometri
 Arcusfunktionerna
Arcusfunktionerna
Om vi känner värdet för #\sin{v},~\cos{v}#, eller #\tan{v}# för en vinkel #v# i en rätvinklig triangel, kan vi bestämma vinkelns storlek med hjälp av arcussinus, arcuscosinus, eller arcustangens.
Dessa är de inversa, eller ”omvända” trigonometriska funktionerna. Oftast betecknas de #\arcsin,~\arccos# och #\arctan#. På många räknare hittar man dem under #\sin^{-1},~\cos^{-1}# och #\tan^{-1}#.
Arcusfuntionerna
I rätvinktiga trianglar gäller
#\arcsin{(\sin{v})}=v\qquad \arccos{(\cos{v})}=v\qquad\arctan{(\tan{v})}=v#
I rätvinktiga trianglar gäller
#\arcsin{(\sin{v})}=v\qquad \arccos{(\cos{v})}=v\qquad\arctan{(\tan{v})}=v#
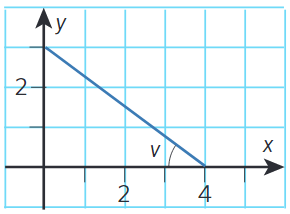
Exempel 1 Bestäm vinkeln #v#.
Lösning
Pythagoras sats ger att den blå sträckans längd är #5#. När alla triangelns sidor är kända kan vi använda valfri arcusfunktion. Vi får
#\sin{v}=\frac{3}{5} \qquad \cos{v}=\frac{4}{5} \qquad \tan{v}=\frac{3}{4} #
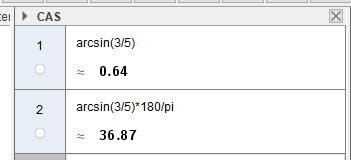
Med något digitalt verktyg kan vi bestämma
#v=\arcsin{\frac{3}{5}}\approx 36,9^{\circ}\qquad v=\arccos{\frac{4}{5}}\approx 36,9^{\circ}\qquad v=\arctan{\frac{3}{4}}\approx 36,9^{\circ}#

Lösning
Pythagoras sats ger att den blå sträckans längd är #5#. När alla triangelns sidor är kända kan vi använda valfri arcusfunktion. Vi får
#\sin{v}=\frac{3}{5} \qquad \cos{v}=\frac{4}{5} \qquad \tan{v}=\frac{3}{4} #
Med något digitalt verktyg kan vi bestämma
#v=\arcsin{\frac{3}{5}}\approx 36,9^{\circ}\qquad v=\arccos{\frac{4}{5}}\approx 36,9^{\circ}\qquad v=\arctan{\frac{3}{4}}\approx 36,9^{\circ}#
Observera att arcusfunktionerna i GeoGebra returnerar vinklar i måttet radianer. Multiplicera värdet med #180/\pi# för att få grader.